Вопрос: Уравнение плоскости в пространстве

· Ах+By+Cz+D=0 – общее уравнение плоскости

· A(X-Xo)+B(Y-Yo)+C(Z-Zo)=0 – уравнение плоскости, проходящей через точку

Mo(Xo,Yo,Zo)перпендикулярно нормальному вектору n(A, B, C)

· – уравнение плоскости в отрезках, где a, b, c – величины направленных oтрезков, отсекаемых плоскостью на координаты осях Ox, Oy, Oz соответственно

· xcos – нормальное уравнение плоскости, где с , cos -- направляющие косинусы нормального вектора n, направленного из начала координат в сторону плоскости, а >0 – расстояние от начала координат до плоскости
Общее уравнение: 1) приводится к нормальному виду 4) путем умножения на нормирующий множитель

Если плоскость Р задана нормальным уравнение вида 4), а M (x, y, z) – некоторая точка пространства, то выражение

Задает отклонение точки M от плоскости. Знак (M,P) указывает на взаимное расположение точки М, плоскости Р и начала координат, а именно: если точка М и начало координат лежат по разные стороны от плоскости Р, то (М,Р)>0, а если М и начало координат находят по одну сторону от плоскости Р, то <0
Расстояние p(M,P) от точки М до плоскости Р определяется равенством
Уравнение плоскости имеет вид (x-1)+(y-1)-2(z-1)=0, или x+y-2z=0. Так как в последнем уравнении отсутствует свободный член, то плоскость проходит через начало координат.
Др.сп-б. Точка М (х, y, z) принадлежит искомой плоскости Р в том и только в том случае, когда векторы ,

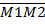
Откуда x+y-2z=0

Поиск по сайту: