АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Первый и второй замечательные пределы

Читайте также:
  1. I-IY Государственные Думы – первый опыт российского парламентаризма.
  2. III.2.1. Первый (ионийский) этап в древнегреческой натурфилософии. Учение о первоначалах мира. Миропонимание пифагореизма
  3. V2: Культура Российской империи второй половины XIX – начала ХХ вв.
  4. XX съезд КПСС. Процесс политической реабилитации и десталинизации во второй половине 1950 – начале 1960-х гг. и его значение.
  5. Актерское искусство второй половины XIX века
  6. Английские колониальные захваты в Индии во второй половине XVIII в.
  7. Антигоспитальное в области психиатрии движение в мире во второй половине XX века
  8. Археологические исследования второй половины XIX – первой трети XX вв. (с.43)
  9. Белорусские города во второй пол 13 – первой пол 17 вв. Развитие ремесла и торговли.
  10. Билет23. Коренной перелом в ходе Великой Отечественной войны и Второй мировой войны.
  11. Болгарская Православная Церковь во второй половине ХХ – начале XXI вв. Церковный раскол в Болгарии.
  12. Боэций: последний из римлян и первый из схоластов

*В лекциях мы кроме, как символьной формулировки первого и второго замечательных пределах не писали, так что они не должны требовать доказательства.

http://www.xn--80aaenbrolc2dd.xn--p1ai/pervyj-i-vtoroj-zamechatelnye-predely/

http://www.bez-dvoek.ru/matem/dif/dif18.html

Здесь вы найдете подробные доказательства.

4.2. Предел функции на бесконечности.

Предел функции на бесконечности. Пусть задана функция у = f(x) с неограниченной сверху областью определения. Число b называется пределом данной функции при х, стремящемся к плюс бесконечности, если для любого числа существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x > M, выполняется неравенство | f(x) – b | < e. Запись этого факта:

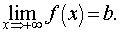
Если область определения данной функции неограниченна снизу, то число b называется пределом данной функции при х, стремящемся к минус бесконечности, если для любого числа e < 0 существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x < –M, выполняется неравенство | f(x) – b | < e. Записывается это так:


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |

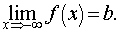
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)