Вопрос: Векторное и смешанное произведение векторов

Векторное: Упорядоченная тройка некомпланарных векторов е1, е2, е3 называется правой, если наблюдателю, находящемуся внутри телесного угла, образованного этими векторами, кратчайшие повороты от е1 к е2 и от е2 к е3 кажутся происходящими против часовой стрелки. В противном случае тройка (е1, е2, е3) называется левой.

Векторным произведением вектора a1 на вектор a2 называется вектор, обозначаемый символом определяемый слудующими тремя условиями:
1) длина вектора 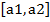равна площади параллелограмма, построенного на векторах а1 и а2, т. е. )

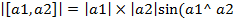2)вектор

3) упорядоченная тройка a1, a2, 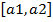правая
Из определения векторного произведения следует, что:

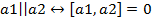
Алгебраические свойства векторного произведения:
1)

2)

3) =

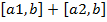
Если вектор а1(X1, Y1, Z1) и a2(X2, Y2, Z2) – векторы заданные своими координатами в правом прямоугольном базисе, то разложение векторного произведения 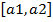в том же базисе имеет вид

Или, в символической записи (с использованием понятия определителя 3его порядка)

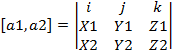
Поиск по сайту: