АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Нахождение наклонной асимптоты

Читайте также:
  1. A)нахождение средней из двух соседних средних, для отнесения полученного результата к определенной дате
  2. Алг «нахождение минимума»
  3. Асимптоты
  4. Асимптоты графика функции
  5. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
  6. Асимптоты графика функции
  7. Асимптоты графика функции.
  8. Асимптоты.
  9. ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ
  10. Вопрос: Бесконечно малые функции и их свойства. Эквивалентные бесконечно малые. Бесконечно большие функции. Вертикальные асимптоты графика функции.
  11. Задание 3Исследование движения тела по наклонной плоскости
  12. Или метод секущих предполагает более быстрое нахождение корня, чем метод половинного деления.

(В условиях существования наклонной асимптоты)

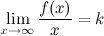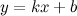Если для функции существуют пределы и , то функция имеет наклонную асимптоту при .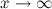

Горизонтальная асимптота является частным случаем наклонной при .

Если при нахождении горизонтальной асимптоты получается, что , то функция может иметь наклонную асимптоту.

Кривая может пересекать свою асимптоту, причем неоднократно.

Пример:

Задание. Найти асимптоты графика функции

Решение. Область определения функции:

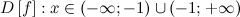
а) вертикальные асимптоты: прямая 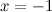- вертикальная асимптота, так как

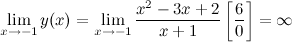
б) горизонтальные асимптоты: находим предел функции на бесконечности:

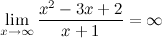
то есть, горизонтальных асимптот нет.

в) наклонные асимптоты :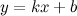

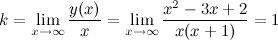
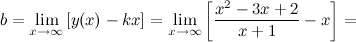
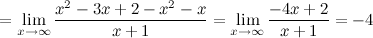
Таким образом, наклонная асимптота: .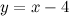

Ответ. Вертикальная асимптота - прямая .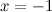

Наклонная асимптота - прямая .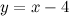


5 Вопрос: Непрерывность функции в точке. Точки разрыва и их классификация.

6 Вопрос: Арифметические действия с непрерывными функциями. Переход к пределу под знаком непрерывной функции.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.007 сек.)