Асимптоты графика функции

Определение. Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

По способам их отыскания выделяют три вида асимптот: вертикальные , горизонтальные 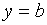, наклонные .

Очевидно, горизонтальные являются частными случаями наклонных (при ).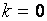

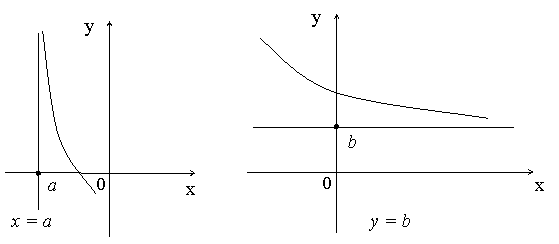
Нахождение асимптот графика функции основано на следующих утверждениях.

Теорема 1. Пусть функция определена хотя бы в некоторой полуокрестности точки и хотя бы один из ее односторонних пределов в этой точке бесконечен, т.е. равен или 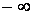. Тогда прямая является вертикальной асимптотой графика функции.

Таким образом, вертикальные асимптоты графика функции следует искать в точках разрыва функции или на концах ее области определения (если это конечные числа).

Теорема 2. Пусть функция определена при значениях аргумента, достаточно больших по абсолютной величине, и существует конечный предел функции . Тогда прямая 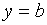есть горизонтальная асимптота графика функции .

Может случиться, что , а , причем и - конечные числа, тогда график имеет две различные горизонтальные асимптоты: левостороннюю и правостороннюю. Если же существует лишь один из конечных пределов или , то график имеет либо одну левостороннюю, либо одну правостороннюю горизонтальную асимптоту.

Теорема 3. Пусть функция определена при значениях аргумента, достаточно больших по абсолютной величине, и существуют конечные пределы и . Тогда прямая является наклонной асимптотой графика функции .

Заметим, что если хотя бы один из указанных пределов бесконечен, то наклонной асимптоты нет.

Наклонная асимптота так же, как и горизонтальная, может быть односторонней.

Поиск по сайту: