Асимптоты

Опр. Часть графика называется бесконечной ветвью если при движении точки по этой части, расстояние между ей и началом координат стремится к бесконечности.

Опр. Прямая называется асимптотой бесконечной ветви графика функции, если при удалении точки от начала координат по этой ветви, расстояние до данной прямой стремится к нулю.

Теорема 1: x=a (вертикальная прямая) – является асимптотой для бесконечно вертикальной ветви графика функции y=f(x), тогда когда f(x)®µ, при x®a.

Теорема 2: Критерий существования наклонной асимптоты прямая y=kx+b является асимптотой для правой (левой) ветви графика функции тогда, когда существует предел при:

Док-во: Точка M0(x0,y0) и прямая

L: Ax+By+Cz=0, то расстояние

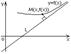Пусть y=kx+b

асимптота =>

d(M,l)®0=>

kx-f(x)+b®0

тогда f(x)-kx®b

при x®+µ

существует предел:

Теорема: Необходимый признак существования наклонной асимптоты. Если прямая l: y=kx+b –

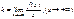наклонная асимп. для правой наклонной ветви, то:

Док-во:

Пример:

x=1 – верт. Асимптота, т.к.

f(x)®µ, когда x®1

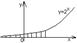
Вывод: y=0×y+1 – наклонная асимптота для левой и правой ветви.

Поиск по сайту: