 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Замечание. Не в каждой своей критической точке функция обязательно имеет максимум или минимум
Не в каждой своей критической точке функция обязательно имеет максимум или минимум.
Необходимое условие экстремума.
Если непрерывная функция  имеет экстремум в точке х0, то ее производная в этой точке равна нулю или не существует.
имеет экстремум в точке х0, то ее производная в этой точке равна нулю или не существует.
Необходимое условие экстремум не является достаточным, т.е. точки, в которых  или же
или же  не существует, не обязательно являются точками экстремумов функции.
не существует, не обязательно являются точками экстремумов функции.
Точки, в которых необходимое условие экстремумов выполняется, называются критическими, или подозрительными на экстремум.
Критические точки входят в область определения функции вместе с некоторой своей окрестностью, в которой функция является непрерывной и дифференцируемой (за исключением, быть может, самой критической точки, где  может не существовать). Критические точки, в которых
может не существовать). Критические точки, в которых  , называются еще стационарными, в них возможен только гладкий экстремум функции
, называются еще стационарными, в них возможен только гладкий экстремум функции 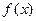 . Критические точки, в которых
. Критические точки, в которых  не существуют, являются подозрительными на острый экстремум функции
не существуют, являются подозрительными на острый экстремум функции 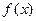 . Наличие или отсутствие экстремума функции в ее критической точке проверяется чаще всего по следующим двум признакам:
. Наличие или отсутствие экстремума функции в ее критической точке проверяется чаще всего по следующим двум признакам:
Первый достаточный признак экстремума.
Если при переходе через критическую точку х0 (слева направо) производная 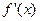 изменяет свой знак, то в точке х0 есть экстремум причем, это максимум, если знак
изменяет свой знак, то в точке х0 есть экстремум причем, это максимум, если знак 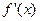 меняется с плюса на минус, и это минимум, если знак
меняется с плюса на минус, и это минимум, если знак 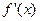 меняется с минуса на плюс. Если при переходе через критическую точку х0 производная
меняется с минуса на плюс. Если при переходе через критическую точку х0 производная 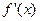 не изменяет свой знак, то в точке х0нет экстремума функции
не изменяет свой знак, то в точке х0нет экстремума функции 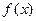 .
.
Второй достаточный признак экстремума.:Пусть х0 – стационарная точка Первый достаточный признак экстремума функции 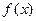 , т.е.
, т.е.  и существует вторая производная
и существует вторая производная  , непрерывная в точке х0.
, непрерывная в точке х0.
Если  >0, то х0 – точка минимума функции
>0, то х0 – точка минимума функции 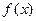 ;
;
если  <0, то х0 – точка максимума функции
<0, то х0 – точка максимума функции 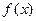 ;
;
если  =0, то вопрос об экстремуме в точке х0 остается открытым.
=0, то вопрос об экстремуме в точке х0 остается открытым.
41). Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х.
Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х.
Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой.

Точка  называется точкой перегиба графика функции y=f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки
называется точкой перегиба графика функции y=f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки 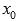 , в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.
, в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.
Другими словами, точка М называется точкой перегиба графика функции, если в этой точке существует касательная и график функции меняет направление выпуклости, проходя через нее.
Если необходимо, обратитесь к разделу касательная к графику функции в точке, чтобы вспомнить условия существования невертикальной и вертикальной касательной.
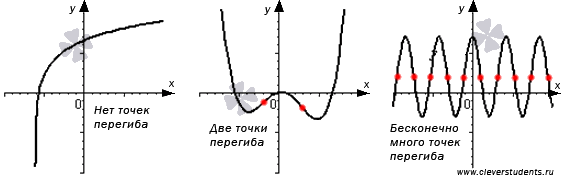
Заметим, что некоторые функции могут не иметь точек перегиба, а другие могут иметь одну, несколько или бесконечно много точек перегиба.
42) Асимптота кривой – это прямая, к которой кривая приближается сколь угодно близко при удалении в бесконечность
Если кривая, заданная уравнением  , удаляется в бесконечность при приближении
, удаляется в бесконечность при приближении  к конечной точке
к конечной точке  , то прямая
, то прямая  называется вертикальной асимптотой этой кривой. Такими асимптотами являются прямая
называется вертикальной асимптотой этой кривой. Такими асимптотами являются прямая  для гиперболы
для гиперболы 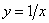 , каждая из прямых
, каждая из прямых 
 для функции
для функции  (рис. 1).
(рис. 1).

Рис. 1
Помимо вертикальной асимптоты  гипербола
гипербола 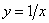 имеет еще и горизонтальную асимптоту
имеет еще и горизонтальную асимптоту  , как и график функции
, как и график функции  , однако он, в отличие от гиперболы, пересекает свою горизонтальную асимптоту в бесконечном множестве точек (рис. 2).
, однако он, в отличие от гиперболы, пересекает свою горизонтальную асимптоту в бесконечном множестве точек (рис. 2).

Рис. 2
У кривой, носящей название «декартов лист» (рис. 3), уравнение которой 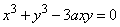 , имеется наклонная асимптота, как и у кривой
, имеется наклонная асимптота, как и у кривой  (рис. 4). Коэффициенты
(рис. 4). Коэффициенты  и
и  в уравнении прямой
в уравнении прямой  , являющейся наклонной асимптотой кривой
, являющейся наклонной асимптотой кривой  при стремлении к плюс или минус бесконечности, находятся как пределы:
при стремлении к плюс или минус бесконечности, находятся как пределы:
 ,
,  .
.
43) СХЕМА ПОЛНОГО ИССЛЕДОВАНИЯ ФУНКЦИИ
1. Найти область определения функции.
2. Исследовать четность и периодичность функции.
3. Исследовать точки разрыва, найти вертикальные асимптоты.
4. Найти наклонные асимптоты (если их существование возможно).
5. Найти точки пересечения графика с осями координат.
6. Найти  . Определить точки экстремума, интервалы возрастания и убывания функции.
. Определить точки экстремума, интервалы возрастания и убывания функции.
7. Найти  . Определить точки перегиба графика, интервалы его выпуклости и вогнутости.
. Определить точки перегиба графика, интервалы его выпуклости и вогнутости.
8. Построить график функции.
Поиск по сайту: