АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Свойства смешанного произведения векторов

Читайте также:
  1. III. Психические свойства личности – типичные для данного человека особенности его психики, особенности реализации его психических процессов.
  2. MathCad: понятие массива, создание векторов и матриц.
  3. V2: ДЕ 14 – Векторные пространства. Коллинеарность векторов.
  4. V2: Электрические и магнитные свойства вещества
  5. Акустические свойства голоса
  6. Акустические свойства строительных материалов
  7. Алгебраические свойства векторного произведения
  8. Алгоритм вычисления произведения
  9. АЛГОРИТМ И ЕГО СВОЙСТВА
  10. Аллювиальные отложения и их свойства
  11. Антигенные свойства антител.
  12. Антитела. Строение, свойства, продукция.
  • Геометрический смысл смешанного произведения.

Модуль смешанного произведения трех векторов a, bи с равен объёму параллелепипеда, образованного этими векторами:

Vпарал = a · [b × c]

Объем пирамиды образованной тремя векторами a, bи с равен одной шестой части от модуля смешанного произведения этих векторов:

Vпир =   |a · [b × c]|
 
  • Если смешанного произведения трех не нулевых векторов равно нулю, то эти вектора компланарные.
  • a · [b × c] = b · (a · c) - c · (a · b)
  • a · [b × c] = b · [c × a] = c · [a × b] = -a · [c × b] = -b · [a × c] = -c · [b × a]

8) Угловой коэффициент прямой — коэффициент в уравнении прямой на координатной плоскости, численно равен тангенсу угла (составляющего наименьший поворот от оси Ox к оси Оу) между положительным направлением оси абсцисс и данной прямой линией

каноническое уравнение прямой на плоскости

 

Нормальное уравнение прямой (рис. 4.11)

 

где - угол, образуемый нормально к прямой и осью Ox; p - расстояние от начала координат до прямой.

Приведение общего уравнения прямой к нормальному виду:

Здесь 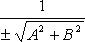- нормируемый множитель прямой; знак выбирается противоположным знаку C, если и произвольно, если C = 0.

9) Если уравнения прямой заданы в общем виде

A 1 x + B 1 y + C 1 = 0,

A 2 x + B 2 y + C 2 = 0

угол между ними определяется по формуле

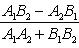
Условия параллельности двух прямых:

а) Если прямые заданы уравнениями с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k 1 = k 2.

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

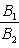
Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.008 сек.)