Геометрический смысл приращения

Посмотрите на следующий рисунок.

Как видите, приращение показывает изменение ординаты и абсциссы точки. А отношение приращения функции к приращению аргумента определяет угол наклона секущей, проходящей через начальное и конечное положение точки.

32)Введем правило для нахождения производной обратной функции.

Теорема. Пусть функция определена на промежутке Х, непрерывна, монотонна (возрастает или убывает) и дифференцируема на Х. Если ее производная в точке не равна нулю, то обратная функция имеет производную в точке 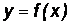, причем

. (4.1)

Доказательство. Функция 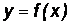определена, непрерывна и монотонна на промежутке Х, тогда она имеет обратную функцию , определенную, непрерывную и монотонную на промежутке Y.

Если значение аргумента получает приращение , отличное от нуля, то в силу монотонности функции функция получает приращение и . В силу непрерывности функции : .

Следовательно,

Итак,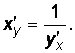

33)

34) Обратное преобразование можно выполнить далеко не всегда. Часто встречаются функции, заданные неявным уравнением, которые невозможно разрешить относительно переменной y. Например, для приведенных ниже функций

невозможно получить зависимость y (x) в явном виде.

Хорошая новость состоит в том, что для нахождения производной y' (x) неявно заданной функции нет необходимости преобразовывать ее в явную форму. Для этого, зная уравнение F (x, y) = 0, достаточно выполнить следующие действия:

Сначала необходимо продифференцировать обе части уравнения по переменной x, предполагая, что y - это дифференцируемая функция x и используя правило вычисления производной от сложной функции. При этом производная нуля (в правой части) также будет равна нулю.

Замечание: Если правая часть отлична от нуля, т.е. неявное уравнение имеет вид

то дифференцируем левую и правую части уравнения.

• Решить полученное уравнение относительно производной y' (x).

35) Геометрический смысл дифференциала

На графике функции возьмем произвольную точку 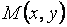и дадим аргументу 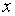приращение . При этом функция получит приращение (на рисунке отрезок ).

Проведем касательную к кривой в точке 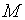и обозначим угол ее наклона к оси через , тогда . Из треугольника находим , т.е. .

Таким образом, дифференциал функции численно равен приращению ординаты касательной, проведенной к графику функции в данной точке, когда аргумент 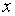получает приращение .

36)Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть или . Тогда, если существует предел отношения производных этих функций 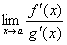, то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

(1)

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

37) Теорема 17.1 (Теорема Ферма)

Если функция имеет производную и в точке 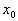имеет экстремум, то значение производной в этой точке равно 0.

Доказательство

Пусть 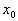- точка минимума. Тогда при . Значение выражения . Значит, . Рассмотрим теперь , при этом также , и выражение . Значит, правая производная 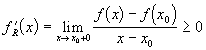. По теореме 14.5 . Из ранее доказанного следует: . Теорема доказана.

Геометрический смысл теоремы Ферма Существует такая точка 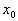, в которой касательная параллельна оси Ox. Замечания В точке экстремума может не быть производной. Пример: , - точка минимума, но .

Равность нулю производной - необходимое условие существования экстремума, но не достаточное. То есть производная может быть равной 0 и вне точки экстремума. Пример: , но точка 0 - не экстремум.

Теорема 17.2 (Теорема Ролля)

Пусть:

Функция непрерывна на отрезке : ;

Для любого x из интервала существует производная: ;

Значения функции на концах отрезка равны: .

Тогда существует такое , что производная .

Доказательство

Функция непрерывна существуют .

Если , то функция является константой, и ее производная в любой точке равна 0, т.е. теорема доказана.

Если же , то оба значения не могут достигаться в концевых точках, т.к. и . Тогда хотя бы одно из них достигается во внутренней точке c, и, по теореме Ферма 17.1

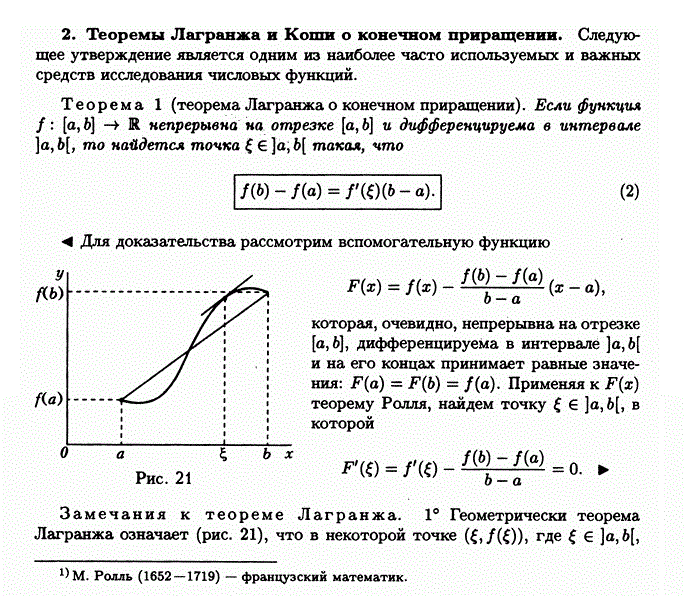
38)

39,40) Точка называется точкой локального максимума функции , если существует такая окрестность этой точки, что для всех из этой окрестности выполняется неравенство: .

Точка называется точкой локального минимума функции , если существует такая окрестность этой точки, что для всех из этой окрестности .

(Необходимое условие экстремума)

Если функция имеет экстремум в точке , то ее производная либо равна нулю, либо не существует.

Точки, в которых производная равна нулю: , называются стационарными точками функции.

Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются критическими точками этой функции. То есть критические точки - это либо стационарные точки (решения уравнения ), либо это точки, в которых производная не существует.

Поиск по сайту: