 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Формула вычисления угла между прямой и плоскостью
Если в пространстве заданы направляющий вектор прямой L
s = {l; m; n}
и уравнение плоскости
Ax + By + Cz + D = 0,
то угол между этой прямой и плоскостью можно найти используя формулу
| sin φ = | | A · l + B · m + C · n | |
| √A2 + B2 + C2 · √l2 + m2 + n2 |
13) В канонической для эллипса системе координат уравнение эллипса имеет вид:
(Свойства эллипса.)
1. В канонической для эллипса системе координат, все
точки эллипса находятся в прямоугольнике
, 
.
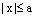2. Точки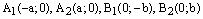 
лежат на
эллипсе.
3. Эллипс является кривой, симметричной относительно
своих главных осей.
4. Центр эллипса является его центром симметрии.
Доказательство. 1, 2) Сразу же следует из канонического уравнения эллипса.
3, 4) Пусть М(х, у) – произвольная точка эллипса. Тогда ее координатыудовлетворяют уравнению (4). Но тогда координаты точек 
также удовлетворяют уравнению (4), и, следовательно, являются точками эллипса, откуда и следуют утверждения теоремы.
Теорема доказана.
14) 
Гипербола представляет собой плоскую кривую, для каждой точки которой модуль разности расстояний до двух заданных точек
Каноническое уравнение гиперболы записывается в виде
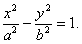
Параболой называется плоская кривая, в каждой точки которой выполняется следующее свойство: расстояние до заданной равно расстоянию до заданной прямой
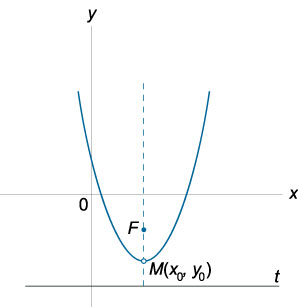
18)Метод Крамера
| ∆ = | = | -259 |
| ∆1 = | = | -722 |
| ∆2 = | = | -12 |
| ∆3 = | = |
| x 1 = | ∆1 | = | -722 | = | ||||
| ∆ | -259 |
| x 2 = | ∆2 | = | -12 | = | ||||
| ∆ | -259 |
| x 3 = | ∆3 | = | = |
| ||||
| ∆ | -259 |
19)Элементарные преобразования по правилу Гаусса-Жордана:
· Смена мест двух строк.
· Умножение всех элементов строки на некоторое число, не равное нулю.
· Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на любой множитель.
20) Для нахождения обратной матрицы запишим матрицу А, дописав к ней справа единичную матрицу:
| 
| ||||
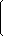
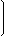
от 2 строк отнимаем 1 строку, умноженую соответственно на 2
|
|
| ||||
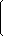
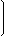
| -3 | -2 |
2-ую строку делим на -3
|
|
| ||||
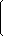
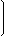
| 2/3 | -1/3 |
от 1 строк отнимаем 2 строку, умноженую соответственно на 2
|
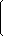
| -1/3 | 2/3 |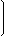
| ||
| 2/3 | -1/3 |
Ответ:
| A-1 = |
| -1/3 | 2/3 |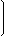
|
| 2/3 | -1/3 |
21)
Исследовать систему алгебраических уравнений (без непосредственного решения системы) с помощью теоремы Кронекера-Капелли.
Запишем систему в виде:
Для удобства вычислений поменяем строки местами:
Добавим 2-ую строку к 1-ой:
Добавим 3-ую строку к 2-ой:
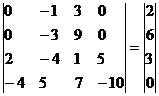
Умножим 3-ую строку на (2). Добавим 4-ую строку к 3-ой:
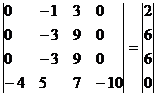
Умножим 1-ую строку на (3). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
Добавим 2-ую строку к 1-ой:
Это соответствует системе:
-3x2 + 9x3 = 6
-4x1 + 5x2 + 7x3 - 10x4 = 0
За базисные переменные примем x1 и x2. Тогда свободные x3,x4.
Поиск по сайту: