 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Адаптивные программы вычисления определенных интегралов
Основная идея адаптивного метода состоит в сравнении двух приближений S1i и S2i и получении при этом оценки их точности. Если точность приемлема, то одно из чисел принимается в качестве значения интеграла по данному подинтервалу. Если точность недостаточна, то подинтервал делится на две или более частей и процесс повторяется для меньших подинтервалов. Если точность значительно меньше требуемой, то на следующем шаге величина подинтервала увеличивается.
Сокращение общего количества вычислений может быть достигнуто также за счет того, что две формулы для расчета S1i и S2i используют значения подинтегральной функции в нескольких общих точках. Например, для формулы Симпсона S2i требует вычисления в пяти точках, три из которых используются при расчете S1i, и поэтому достаточно вычислить только два новых значения функции f(x).
Для формулы Симпсона сокращение интервала вдвое увеличивает точность вычисления приблизительно в 16 раз.
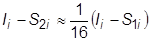 .
.
Выразим отсюда неизвестную величину Ii – S2i:
 .
.
Проводя подобные вычисления для формул прямоугольников или трапеций, получим оценку погрешности
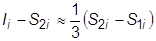 .
.
Разность между истинным значением и результатом вычисления с уменьшенным вдвое шагом оказывается меньше, чем разность между результатами расчета с первоначальным и половинным шагом. Поэтому, если на каждом шаге обеспечить выполнение условия
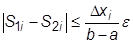 ,
,
то при суммировании всех интервалов будем иметь
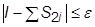 .
.
На рис. 24.1 приведена блок-схема адаптивного алгоритма вычисления определенного интеграла методом средних прямоугольников. В начале программы в качестве шага интегрирования выбирается длина всего диапазона интегрирования. Далее по двум формулам с целым и половинными шагами рассчитываются значения интеграла на участке шириной D x.

|
При обеспечении требуемой точности расчета полученное значение S2i суммируется с вычисленными ранее на предыдущих интервалах и делается следующий шаг.
Если точность расчета заметно (в приведенной схеме в 20 раз) превышает требуемую, длина шага увеличивается в 1,87 раза. В том случае, если погрешность расчета оказывается чрезмерной, длина шага уменьшается вдвое.
Коэффициенты увеличения и уменьшения шага выбраны не кратными друг другу для более гибкого изменения длины шага интегрирования. В зависимости от вида подинтегральной функции и желания программиста эти величины могут быть выбраны несколько иными.
22 Вычисление определенных интегралов в среде Excel
Поиск по сайту: