Вычисление определенных интегралов методом прямоугольников

Определенный интеграл функции f (x) на отрезке [ a,b ] можно представить как площадь под кривой f (x), ограниченной пределами интегрирования и осью абсцисс. Разобьем отрезок [ a,b ] на n отрезков одинаковой длины

.

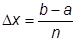В результате получим набор равноудаленных друг от друга точек 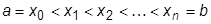. Рассмотрим один отрезок [ x_i-1,x_i ].

Для аппроксимации функции f (x) будем использовать полином нулевой степени , где - некоторая постоянная величина, ограниченная значениями
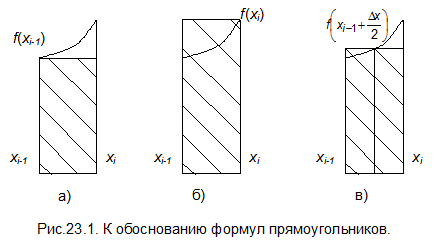
f (x_i-1) и f (x_i). Если принять, что величина равна значению f (x_i-1) на левом крае отрезка, то площадь криволинейной трапеции будет приблизительно равна площади заштрихованного на рис.23.1.а прямоугольника

.

Сумма площадей всех прямоугольников даст приближенное значение интеграла:

. (23.1)

Это формула левых прямоугольников.

В качестве величины 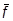можно взять значение функции на правой границе отрезка f (x_i). Площадь заштрихованного прямоугольника на рис.23.1.б будет равна

,

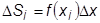а значение интеграла:

. (23.2)

Это формула правых прямоугольников.

Если вычислять значение функции не на краях, а в середине интервала, то, согласно рис.23.1.в, можно ожидать увеличения точности, поскольку завышенные значения площади по сравнению с истинными на одной стороне прямоугольника компенсируются заниженными значениями на другой стороне. Площадь заштрихованного прямоугольника будет равна

,

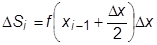а величина интеграла:

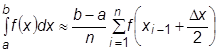. (23.3)

Это формула средних прямоугольников.

Блок-схема метода прямоугольников с заданным количеством разбиений приведена на рис. 23.2.

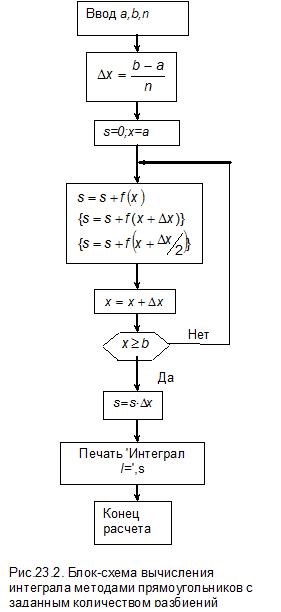
Для начала расчета задаются границы интегрирования [ a,b ] и количество подинтервалов n, на которые разбивается основной интервал. Затем в соответствии с выбранным методом интегрирования суммируются значения функции на каждом из подинтервалов. Поскольку длины подинтервалов равны между собой, то величину D x целесообразно вынести за знак суммы и умножить на эту величину окончательную сумму значений функций.

Сумма длин подинтервалов точно равна общей длине интервала интегрирования, поэтому в этом алгоритме не нужен контроль за совпадением концов последнего подинтервала и всего интервала.

В некоторых случаях более удобно задавать не количество разбиений, а шаг интегрирования D x. При этом величина D x может быть не кратной длине интервала интегрирования, поэтому на последнем шаге необходима проверка совпадения длин и при необходимости корректировка величины D x. Поскольку D x может измениться, то его нельзя выносить за знак суммы.

Блок-схема метода приведена на рис.23.3.

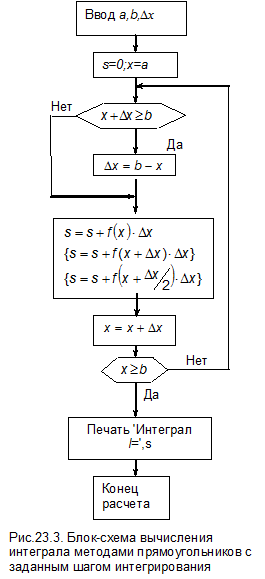
Поиск по сайту: