Алгоритм решения ЗЛП графическим методом

1. Находим область допустимых решений системы ограни­чений задачи.

2. Строим вектор-градиент .

3. Проводим линию уровня L ₀, которая перпендикулярна вектору .

4. Линию уровня перемещаем по направлению вектора параллельно себе пока она не станет опорной к многоугольнику планов. Точка входа в область – точка минимума функции, точка выхода из области – точка максимума.

Если только одна общая точка с областью допусти­мых решений, то эта точка будет точкой экстремума и решение ЗЛП единственное.

Если окажется, что линия уровня проходит через одну из сторон ОДР, то в таком случае экстремум достигается во всех точках соответствующей стороны, а ЗЛП будет иметь бесчисленное множество решений. Говорят, что такая ЗЛП имеет альтернативный оптимум, и ее решение находят в виде выпуклой линейной комбинации решений :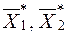

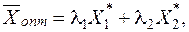
где .

ЗЛП может быть неразрешима, когда определяющие ее ограничения окажутся противоречивыми (т. е. область допустимых решений окажется пустым множеством).

5. Находим координаты точки экстремума и значение це­левой функции в этой точке.

Пример 38.1. Найти максимум функции , если

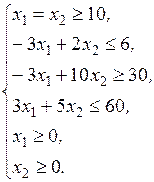
Решение.

Определим вначале многоугольник решений – ОДР.

Для этого построим прямые, которые ограничивают этот многоугольник:

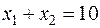I: ; II: ;

III: 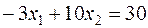; IV: .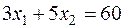

Каждая прямая отсекает отрезки на осях координат: I – (10;10); II – (-2;3); III – (-10;3); IV – (20;12).

Проверим справедливость каждого неравенства по одной точке (начало координат).

Рассмотрим первое неравенство: 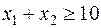. Начало координат (0;0) не удовлетворяет этому неравенству, поэтому область решения лежит по другую сторону от прямой I; это показано на рис. 38.4 стрелками.

Для второго неравенства начало координат (0;0) удовлетворяет этому неравенству, поэтому область решения лежит по ту же сторону от прямой II, что и начало координат.

Рассмотрим неравенство 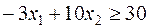. Начало координат (0;0) не удовлетворяет этому неравенству, поэтому область решения лежит по другую сторону от прямой ІII.

Рассмотрим неравенство . Начало координат (0;0) удовлетворяет этому неравенству, поэтому область решения лежит по ту же сторону от прямой IV, что и начало координат.

Замечание: Если ограни- чивающая прямая проходит через начало координат, то вместо точки (0;0) можно взять любую другую точку.

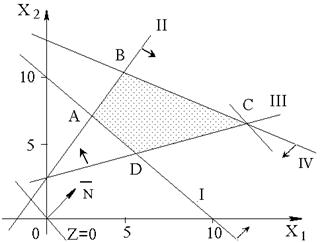
Рис. 38.4. Многоугольник решений

Образовалась область решения всех неравенств – это многоугольник АВСД – многоугольник планов.

Теперь строим градиент целевой функции. Это вектор: = .

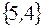Далее строим линию уровня, соответствующую 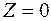; она проходит через начало координат и перпендикулярна . Перемещая ее в направлении вектора , видим, что наиболее отдаленной вершиной многоугольника является вершина С.

Вычислим координаты этой вершины. Точка С лежит на пересечении прямых IIIи ІV. Решим систему уравнений этих прямых:

Откуда

Следовательно,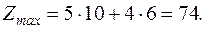

Пример 38.2. Найти минимум функции 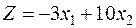, если

Решение.

Для построения многоугольника решений можно использовать пример 38.1. Далее строим градиент целевой функции (рис. 38.5).

Это вектор: = .

Строим линию уровня 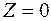, она проходит через начало координат и перпендикулярна . Пе­ремещая ее в направлении вектора = , видим, что вектор является нормальным вектором прямой III, значит линия уровня и прямая III параллельны, то есть при входе в область линия уровня совпадает с прямой DС.

38.5. Многоугольник решений

Вычислим координаты точек D и С, а также значение функции цели. Точка D лежит на пересечении прямых І и III. Решим систему уравнений:

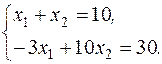
Откуда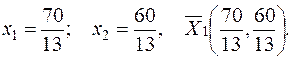

Тогда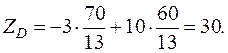

Точка С лежит на пересечении прямых III и IV. Решим систему уравнений:

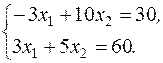
Откуда ,

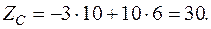
Следовательно, минимум будет в любой точке отрезка DС:

где .

.

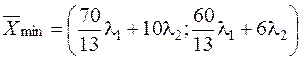Поиск по сайту: