АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Алгоритм. 1.Выписать для системы матрицу коэффициентов и вектор правой части

Читайте также:
  1. XII. ЭЛЕМЕНТЫ ТЕОРИИ АЛГОРИТМОВ
  2. Алгоритм
  3. Алгоритм
  4. Алгоритм
  5. Алгоритм 65 «Кровотечение в послеродовом периоде»
  6. Алгоритм 72 «Ожоги и травмы глаза, века, конъюнктивы»
  7. Алгоритм MD4
  8. Алгоритм RC6
  9. Алгоритм RSA
  10. Алгоритм Брезенхема для окружности
  11. Алгоритм Брезенхема.

1. Выписать для системы матрицу коэффициентов 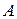и вектор правой части .

2. Преобразовать исходную систему к виду , где элементы матрицы 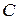определяются по формулам:

,
,
элементы столбца :

.

3. Проверить условие сходимости: имеет ли матрица 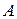диагональное преобладание или в преобразованной системе уравнений имеет ли норма матрицы коэффициентов значение, меньшее единицы 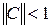(в качестве нормы можно взять евклидову норму ).

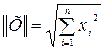4. Задать вектор нулевого приближения .

5. Вычислить координаты вектора следующего, более точного приближения к решению по итерационной формуле:

или

6. Окончание итерационного процесса:

- оценить погрешность ;

- итерационный процесс заканчивается, как только .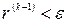


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)