АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Вычисление определенных интегралов методом трапеций

Читайте также:
  1. Абсолютная и условная сходимость несобственных интегралов.
  2. Адаптивные программы вычисления определенных интегралов
  3. Алгоритм решения ЗЛП графическим методом
  4. Алгоритм решения систем линейных уравнений методом Жордана-Гаусса
  5. Анализ движения денежных средств прямым и косвенным методом
  6. Анализ методом деревьев событий и отказов
  7. Б) Вычисление тригонометрических функций.
  8. В определенных условиях ВЗД способны обеспечить ощутимую экономию.
  9. Векторное и смешанное произведение векторов. Свойства и геометрический смысл. Вычисление через координаты векторов.
  10. Вибір оптимального варіанта СМ методом мікровартостей
  11. Визначення осмотичного тиску клітинного соку плазмолітичним методом
  12. Визначення параметрів емпіричної формули за методом найменших квадратів.

Если для аппроксимации функции f (x) взять полином первой степени и поставить условие, чтобы значения функций f (x) и j(x) совпадали на концах подинтервалов, то заштрихованная площадь на рис.3.4. будет равна

,

а вся площадь под кривой, соответствующая значению определенного интеграла,

. (23.4)

Это формула трапеций.

Вычисления по методу трапеций также могут быть организованы как с заданным количеством подинтервалов n, так и с заданной величиной шага D x. В блок-схемах алгоритмов на рис.23.2 и рис.23.3 изменится только узел вычисления интегральной суммы:

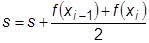
или, например, организован цикл:

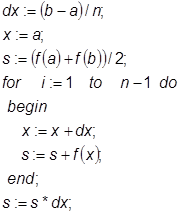
Метод трапеций удобно применять, когда подинтегральная функция задана табличным способом и известны значения функции только на границах подинтервалов.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)