Метод половинного деления (метод дихотомии)

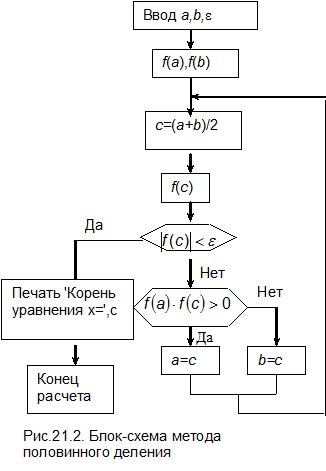
Приближенные значения корней уточняют различными итерационными методами, предполагающими последовательное приближение к искомому значению при выполнении однотипных операций. Если заранее известен интервал [ a,b ], на котором функция меняет знак, т.е. выполняется условие , то наиболее надежным является метод половинного деления. Блок-схема метода приведена на рис. 21.2.

Для определения корня этим методом необходимо указать интервал [ a,b ], на котором функция меняет знак, и допустимую погрешность e. Затем вычисляются значения функции на границах интервала f (a) и f (b). После этого организуется цикл, в котором вычисляются середина интервала c= (a+b)/ 2 и значение функции f (c). Далее проверяется условие . При его выполнении принимается, что точка с является корнем уравнения, на экран выводится соответствующее сообщение и расчет прекращается. Если значение функции в точке с по абсолютной величине превосходит допустимую погрешность e, то из двух половин выбирается та, на которой функция меняет знак, и цикл повторяется.

Метод половинного деления прост и надежен, к корню расчет сходится при любых непрерывных функциях f (x), в том числе и недифференцируемых, при этом метод устойчив к ошибкам округления. Скорость сходимости невелика, за одну итерацию интервал неопределенности [ a,b ] сокращается вдвое, зато точность расчета гарантируется.

Недостатки метода:

1. Для начала расчета необходимо найти отрезок, на котором функция меняет знак.

2. Если на этом отрезке несколько корней, то заранее неизвестно, к какому из корней сойдется процесс, хотя к одному из них обязательно сойдется.

3. Метод не применим для решения систем уравнений.

Метод половинного деления используется, когда требуется высокая надежность счета, а скорость сходимости малосущественна.

Поиск по сайту: