Выбор шага интегрирования по заданной точности

Погрешность метода средних прямоугольников при вычислениях с постоянным шагом D x оценивается величиной

,

где - вторая производная функции f (x).

Погрешность метода трапеций приблизительно равна

.

В общем случае погрешность формулы средних прямоугольников примерно вдвое меньше, чем у формулы трапеций. Поэтому, если значения функции одинаково легко определяются в любых точках, то лучше вести расчет по более точной формуле средних прямоугольников. Метод трапеций употребляют в тех случаях, когда функция задана только в узлах сетки, а в середине интервала ее значения неизвестны.

Главные члены погрешностей у формул средних прямоугольников и трапеций имеют различные знаки, поэтому, если вести расчеты по обеим формулам, точное значение интеграла будет, как правило, находиться в вилке между ними. Используя это свойство, можно добиться повышения точности расчетов. Так как

, ,

то, применяя комбинированную формулу

,

сократим основные источники погрешностей. Подставляя в нее конкретные значения, получим формулу

,

соответствующую методу Симпсона, погрешность которого оценивается величиной

.

В методах средних прямоугольников и трапеций уменьшение шага интегрирования D x вдвое уменьшает погрешность оценки площади элементарного прямоугольника в 8 раз, однако, общее количество этих прямоугольников увеличивается в 2 раза, поэтому общая погрешность уменьшается приблизительно в 4 раза. Коэффициент уменьшения ошибки пропорционален величине второй производной и обычно не равен в точности 4, поскольку не является константой и сказывается также влияние членов более высокого порядка. Однако, при реальных вычислениях с функциями, имеющими непрерывные ограниченные вторые производные, можно ожидать, что удвоение числа элементарных отрезков для любой формулы – средних прямоугольников или трапеций – приблизительно учетверяет точность.

Если в методе Симпсона уменьшить шаг D x в два раза, то каждое Dх⁵ уменьшится в 32 раза, при этом общее количество элементарных фигур возрастет в 2 раза. Погрешность в целом уменьшится приблизительно в 16 раз.

При выборе количества разбиений n или величины шага D x заранее неизвестно, какова будет погрешность вычисления интеграла. Кроме того, точное значение интеграла также неизвестно и сравнить полученное значение с точным нельзя.

Для оценки точности вычисления сравнивают два последовательных приближения к результату. Сначала задают некоторое начальное n₁, для которого вычисляют приближенное значение S₁. Затем число участков удваивают, n₁ =2 n₁, соответственно длины участков сокращаются вдвое, . Далее вычисляют новую сумму площадей более узких фигур S₂. Она точнее приближает искомое значение интеграла. Разность 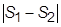сравнивают с наперед заданным малым положительным числом e. При считают, что S₂ можно принять за приближенное значение интеграла, полученное с заданной точностью e. В противном случае процесс деления отрезков повторяют, принимая n₃=2n₂, вычисляют S₃ и сравнивают с e.

Для непрерывных функций условие должно наступить обязательно, если e>e_маш. Следует отметить, что выполнение условия в общем случае не означает, что погрешность вычисления интеграла меньше величины e. Здесь сравнивается окончательное значение S_k не с точным значением, а с вычисленным ранее при более крупном шаге интегрирования. Тем не менее, для многих функций такая оценка величины погрешности является достаточной.

При численном интегрировании величина погрешности зависит не только от используемого метода, но и от вида интегрируемой функции. Основным способом уменьшения погрешности вычисления интеграла является уменьшение ширины элементарного отрезка Dх, т.е. увеличение количества разбиений. Однако это приводит к увеличению объема вычислений и соответственно к увеличению продолжительности счета.

Вместе с тем влияние ширины отрезка Dх на точность расчета может быть неодинаковым на разных участках интегрирования. Если функция на некотором участке изменяется мало или ее вид близок к виду аппроксимирующей функции j(х), то для обеспечения требуемой точности целесообразно проводить вычисления с более крупным шагом. Там, где функция изменяется более быстро, целесообразно уменьшать шаг интегрирования.

Для обеспечения выбора приемлемого шага интегрирования на участке в зависимости от выбора типа метода интегрирования и поведения подинтегральной функции применяются адаптивные программы, построенные на алгоритмах с одной или двумя функциями, автоматически определяющими величину шага.

Пользователь подобной программы указывает конечный интервал [ a,b ] и допустимую погрешность e. Программа пытается вычислить величину S, такую, что

.

В процессе вычислений интервал [ a,b ] разбивается на подинтервалы [ x_i-1,x_i ]. В большинстве программ новый подинтервал получается делением пополам подинтервала, полученного на более раннем этапе вычисления. Реальное число подинтервалов и их длина зависят от функции f(x) и требуемой точности e.

Типичная схема применяет к подинтервалу две различные формулы. Например, схемы, основанные на формуле Симпсона, используют основную формулу с двумя элементарными отрезками

и составную формулу с четырьмя элементарными отрезками

.

Выражения S_1i и S_2i являются приближениями к величине интеграла

.

Поиск по сайту: