Вычисление производной по трем точкам

Для расчета второй производной необходимо, как минимум, уже три точки.

. (28.9)

Для равноотстоящих узлов, когда x ₂- x ₁= х ₁- х ₀= h, получаем

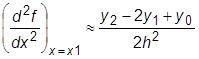. (28.10)

При выборе типа аппроксимации следует исходить из того, что вычисление по формулам более высокого порядка не всегда дает положительный эффект. Во-первых, расчет по более сложным формулам охватывает большее количество точек и требует большего объема машинной памяти, большего времени вычисления и поэтому он менее экономичен. Во-вторых, формулы более высокого порядка заметно эффективнее только при мелкой сетке, когда шаги дифференцирования x ₂- x ₁, х ₁- х ₀, относительно малы. В случае грубой сетки преимущество в точности быстро уменьшается.

С одной стороны ясно, что для увеличения точности вычислений необходимо стремиться к уменьшению шага дифференцирования. Это возможно только в том случае, если имеется возможность вычислять значения функции f (x) для любого х. При табличном представлении функции f (x) такая возможность отсутствует. С другой стороны, при наличии погрешностей в значениях функции уменьшение шага дифференцирования может привести даже к увеличению погрешности определения производной. При этом на точность расчета может существенным образом повлиять выбор порядка аппроксимирующего многочлена. Превосходство формул высокого порядка зависит от гладкости функций. Если есть разрывы функций или случайные колебания, то погрешности у формул высокого порядка могут оказаться выше, чем при использовании формул более низкого порядка.

Поиск по сайту: