Вычисление определенного интеграла

Пусть в определенном интеграле 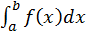нижний предел закреплен, а верхний предел меняется. Тогда будет меняться и значение интеграла, т.е. интеграл станет функцией верхнего предела. Для того, чтобы иметь привычные обозначения, верхний предел обозначим через а чтобы не смешивать его с переменной интегрирования, последнюю обозначим через т.к. от обозначения переменной интегрирования значение интеграла не зависит. Получим интеграл 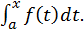При постоянном этот интеграл будет представлять собой функцию верхнего предела Эту функцию мы обозначим через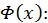

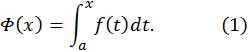
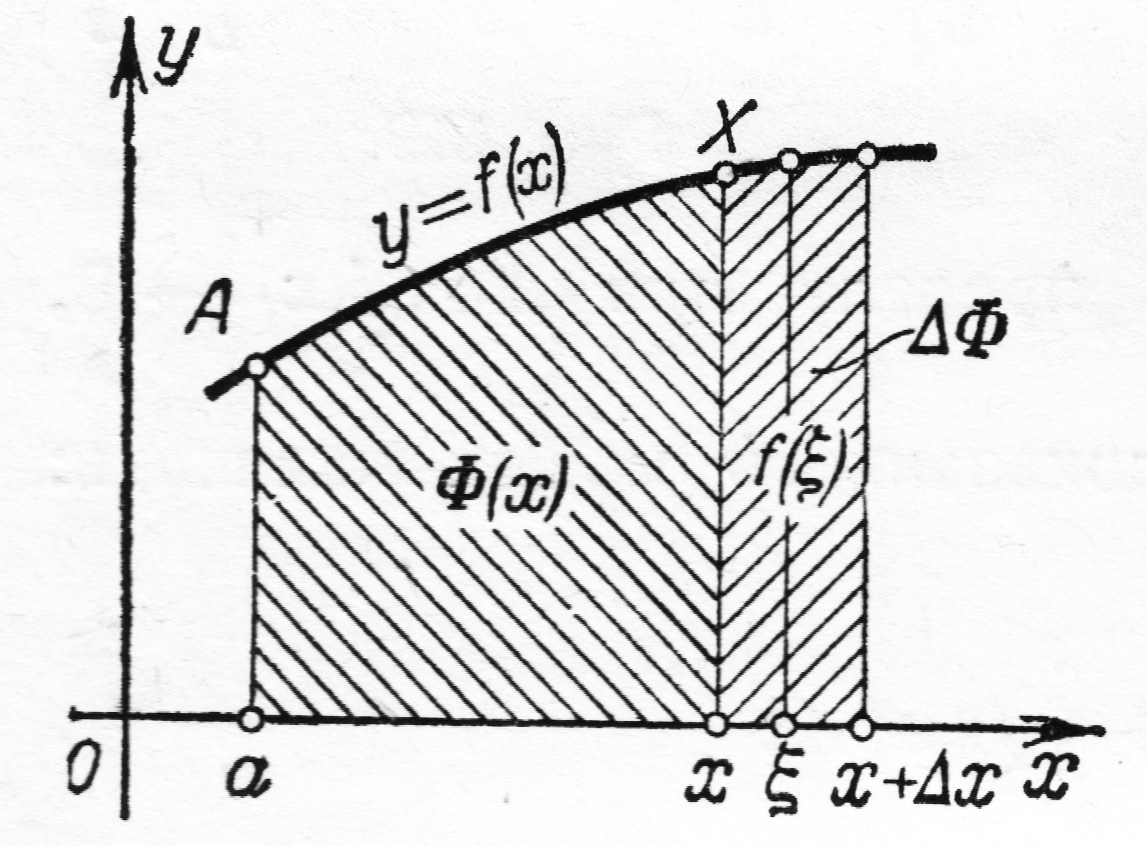
Если 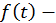неотрицательная функция, то величина 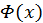численно равна площади криволинейной трапеции 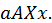Очевидно, что эта площадь изменяется в зависимости от изменения 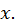Найдем производную от 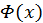по т.е. найдем производную определенного интеграла (1) по верхнему пределу.

Теорема 1. Если непрерывная функция и 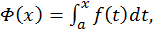то имеет место равенство

Иными словами, производная от определенного интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела (при условии, что подынтегральная функция непрерывна).

Доказательство. Дадим аргументу приращение 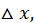тогда (учитывая свойство 8 определенного интеграла) получим:

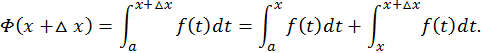
Приращение функции 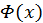равно:

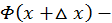
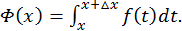
Применим теперь теорему о среднем (свойство 7 определенного интеграла):

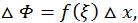где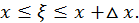

Найдем отношение приращения функции к приращению аргумента:

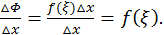
Следовательно,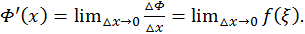

Но, т.к. 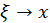при то

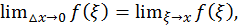
а вследствие непрерывности функции

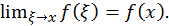
Таким образом, Ч.т.д.

Из доказанной теоремы, в частности, следует, что всякая непрерывная функция имеет первообразную.

Теорема 2. Если 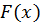есть какая-либо первообразная от непрерывной функции 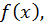то справедлива формула

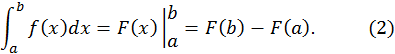
Эта формула называется формулой Ньютона – Лейбница.

Доказательство. Пусть 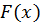есть некоторая первообразная от функции 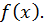По теореме 1 функция 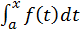есть также первообразная от 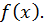Но две любые первообразные от данной функции отличаются на постоянное слагаемое С. Следовательно, можно написать:

Это равенство при соответствующем выборе С справедливо при всех значениях т.е. является тождеством. Для определения постоянного С положим в этом тождестве тогда

откуда 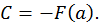Следовательно,

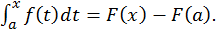
Полагая 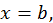получим формулу Ньютона – Лейбница:

или, заменив обозначение переменной интегрирования на

Формула Ньютона – Лейбница дает практически удобный метод вычисления определенных интегралов в том случае, когда известна первообразная подынтегральной функции.

Поиск по сайту: