Ряды Тейлора и Маклорена

Мы с вами уже знаем, что для функции 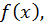имеющей все производные до го порядка включительно в окрестности точки (т.е. на некотором интервале, содержащем точку ), справедлива формула Тейлора:

где остаточный член.

Если функция имеет производные всех порядков в окрестности точки то в формуле Тейлора число можно брать сколь угодно большим. Допустим, что в рассматриваемой окрестности остаточный член при Тогда, переходя в формуле к пределу при получим справа бесконечный ряд, который называется рядом Тейлора:

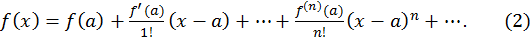
Эта формула справедлива лишь в том случае, если при В этом случае написанный справа ряд сходится и его сумма равна данной функции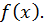

Если в ряде Тейлора положим то получим частный случай ряда Тейлора – ряд Маклорена:

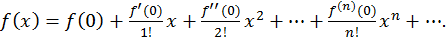
Отметим, что для каждой из элементарных функций существует такое и такое что в интервале она разлагается в ряд Тейлора или в ряд Маклорена.

Пример 1.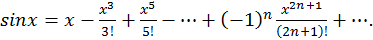

Так как остаточный член стремится к нулю при любом то данный ряд сходится и имеет в качестве суммы функцию при любом

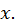
Пример 2.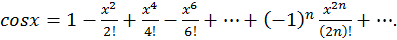

При всех значениях ряд сходится и представляет функцию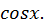

Пример 3.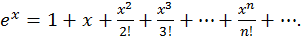

Так как 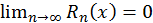для любого то для всех значений ряд сходится и представляет функцию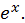

Пример 4.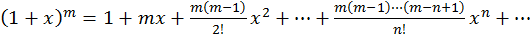

Ряд сходится и представляет функцию для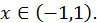

Пример 5.

Ряд сходится и представляет функцию для

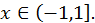
Функции нескольких переменных

Лекция 23.

При изучении многих явлений приходится иметь дело с функциями двух, трех и более переменных. Приведем примеры.

Пример 1. Площадь 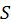прямоугольника со сторонами, длины которых равны и 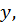выражается формулой: 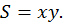Каждой паре значений и соответствует определенное значение площади 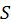есть функция двух переменных.

Пример 2. Объем прямоугольного параллелепипеда с измерениями есть функция трех переменных.

Если каждой паре значений двух, независимых друг от друга, переменных величин и 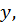из некоторой области их изменения соответствует определенное значение величины 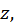то 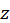есть функция двух независимых переменных и 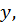определенная в области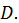

Символически функция двух переменных обозначается так и т. д. Пару значений называют часто точкой 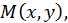а функцию двух переменных – функцией точки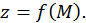

Функция двух переменных может быть задана, например, в виде таблицы с двумя входами или аналитически – с помощью формулы, как это было сделано в примерах.

Функция двух переменных существует, вообще говоря, не при любых значениях и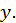

Совокупность пар значений и 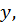при которых определяется функция называется областью определения этой функции.

Область определения функции наглядно иллюстрируется геометрически. Если каждую пару значений и мы будем изображать точкой в плоскости то область определения функции изобразится в виде некоторого множества точек на плоскости. Это множество точек будем также называть областью определения функции. Областью определения может быть вся плоскость или часть плоскости, ограниченная линией. Линию, ограничивающую данную область, будем называть границей области. Точки области, не лежащие на границе, будем называть внутренними точками области. Область, состоящая из одних внутренних точек, называется открытой или незамкнутой. Если же к области относятся и точки границы, то область называется замкнутой. Область называется ограниченной, если существует такое постоянное 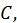что расстояние любой точки области от начала координат 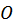меньш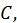е т.е.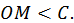

Примеры нахождения области определения функции.

1)

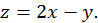
Аналитическое выражение имеет смысл при любых значениях и 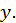Следовательно, областью определения функции является вся плоскость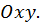

2)

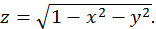
Для того, чтобы 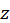имело действительное значение, нужно, чтобы под корнем стояло неотрицательное число, т.е. и должны удовлетворять неравенству: или Областью определения функции является множество всех точек 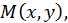координаты которых удовлетворяют указанному неравенству, т.е. лежат в круге радиуса 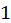с центром в начале координат и на границе этого круга.

3)

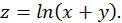
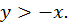Так как логарифмы определены только для положительных чисел, то должно удовлетворяться неравенство или Областью определения функции является полуплоскость, расположенная выше биссектрисы второй и четвертой четвертей, причем сама биссектриса не входит в нее.

Определение функции двух переменных легко обобщить на случай трех и более переменных.

Геометрическое изображение функции двух переменных

Рассмотрим функцию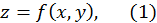

определенную в области 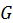на плоскости (эта область может быть и всей плоскостью), и систему прямоугольных координат В каждой точке восставим перпендикуляр к плоскости и на нем отложим отрезок, равный Тогда мы получим в пространстве точку с координатами Множество точек координаты которых удовлетворяют уравнению называется графиком функции двух переменных.

Из аналитической геометрии мы знаем, что уравнение в пространстве определяет некоторую поверхность. Таким образом, графиком функции двух переменных является поверхность, проектирующаяся на плоскость в область определения функции.

Пример. Графиком функции как известно из аналитической геометрии, является параболоид вращения.

Геометрические изображения функций трех и большего числа переменных не имеют простого геометрического смысла.

В некоторых случаях можно получить наглядное геометрическое представление о характере изменения функции, рассматривая ее линии уровня (или поверхности уровня), т.е. линии (или поверхности), где данная функция сохраняет постоянное значение.

Линией уровня функции 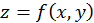называется множество всех точек плоскости для которых данная функция имеет одно и то же значение (изокривая). Таким образом, уравнение линии уровня есть 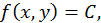где 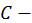некоторая постоянная. Придавая 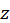постоянные значения мы получим в плоскости линии уровня Геометрически они получаются, если пересекать поверхность плоскостями, параллельными плоскости и проектировать линии пересечения на эту плоскость.

Этот способ, в частности, широко применяется при черчении географических карт; там функцией служит высота над уровнем океана.

Полученная система линий уровня может иметь вид, например, изображенный на рисунке; маленькие черточки указывают направление убывания функции от линии уровня, для географической карты это – направление стока воды. Из рисунка видно, что рассматриваемый график имеет 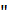вершины 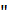в точках и (причем в более высокую), в точке перевал и т.п.

Поверхностью уровня функции называется множество всех точек пространства для которых данная функция имеет одно и то же значение (изоповерхность).

Линии и поверхности уровня постоянно встречаются в физических вопросах. Например, соединив на карте поверхности Земли точки с одинаковой средней суточной температурой или с одинаковым средним суточным давлением, получим соответственно изотермы и изобары, являющиеся важными исходными данными для прогноза погоды.

Поиск по сайту: