Степенные ряды.Теорема Абеля

Степенным рядом называется функциональный ряд вида

где постоянные числа, называемые коэффициентами ряда.

Теорема 1 (теорема Абеля).

1) Если степенной ряд сходится при некотором значении не равном нулю, то он абсолютно сходится при всяком значении для которого

2) если ряд расходится при некотором значении то он расходится при всяком для которого

Доказательство. 1) Так как, по предположению, числовой ряд

Сходится, то его общий член при а это значит, что существует такое число что все члены ряда по абсолютной величине меньше

Перепишем ряд в виде:

и рассмотрим ряд из абсолютных величин его членов

Члены этого ряда меньше соответствующих членов ряда

При члены последнего ряда составляют геометрическую прогрессию со знаменателем и, следовательно, этот ряд сходится. Так как члены ряда 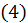меньше соответствующих членов ряда то ряд 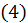тоже сходится, а это и значит, что ряд 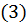или сходится абсолютно.

2) Докажем вторую часть теоремы: пусть в некоторой точке ряд расходится. Тогда он будет расходиться в любой точке удовлетворяющей условию Действительно, если бы в какой-либо точке удовлетворяющей этому условию, ряд сходился, то, в силу только что доказанной первой части теоремы, он должен был бы сходиться и в точке т.к. Но это противоречит условию, что в точке ряд расходится. Следовательно, ряд расходится и в точке 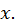Таким образом, теорема полностью доказана.

Теорема Абеля позволяет судить о расположении точек сходимости и расходимости степенного ряда. Действительно, если есть точка сходимости, то весь интервал заполнен точками абсолютной сходимости. Если точка расходимости, то вся бесконечная полупрямая вправо от точки и вся полупрямая влево от точки состоят из точек расходимости. Из этого можно заключить, что существует такое число что при мы имеем точки абсолютной сходимости и при точки расходимости. Таким образом, имеет место следующая теорема о строении области сходимости степенного ряда.

Теорема 2. Областью сходимости степенного ряда является интервал с центром в начале координат.

Интервалом сходимости степенного ряда называется такой интервал от до что для всякой точки лежащей внутри этого интервала, ряд сходится и притом абсолютно, а для точек лежащих вне его, ряд расходится. Число называют радиусом сходимости степенного ряда. На

концах интервала (т.е. при и при ) вопрос о сходимости или расходимости данного ряда решается особо. У некоторых рядов интервал сходимости вырождается в точку у других охватывает всю ось

Часто радиус сходимости степенного ряда может быть определен с помощью признака Даламбера.

Для этого рассмотрим ряд, составленный из абсолютных величин членов ряда

Как мы знаем, если ряд 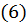сходится, то будет сходиться и ряд и при этом абсолютно. А для решения вопроса о сходимости ряда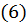

можно воспользоваться признаком Даламбера, т.к. этот ряд является рядом с положительными членами.

Пример 1.

Ряд сходится, если т.е. если

При ряд сходится, при ряд расходится.

Итак, ряд сходится в полузамкнутом интервале

Пример 2.

Так как предел не зависит от и меньше единицы, то ряд сходится при всех значениях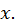

Ряды по степеням

Степенным рядом также называется функциональный ряд вида:

где постоянные также называются коэффициентами ряда.

Для определения области сходимости ряда произведем в нем замену переменного После этой замены ряд примет вид

т.е. получили знакомый нам степенной ряд, расположенный по степеням Пусть ряд имеет интервал сходимости Отсюда следует, что ряд будет иметь интервал сходимости

Таким образом, изучение рядов сводится к изучению рядов

Поиск по сайту: