Площадь криволинейного сектора в полярных координатах

Рассмотрим криволинейный сектор ограниченный линией, заданной уравнением в полярных координатах, лучами

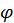Сектор разобьем произвольным образом на частичных секторов обозначим через Каждый из частичных секторов заменим круговым сектором с радиусом где значение угла из промежутка и центральным углом Площадь последнего сектора выражается формулой:

Сумма

Выражает площадь 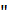ступенчатого 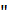сектора (веерообразной фигуры), аппроксимирующего данный сектор

Площадью сектора называется предел площади 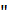ступенчатого 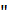сектора при

Пример. Вычислить площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда: где положительное число.

Круг радиуса имеет площадь т.е. площадь площади круга с радиусом, равным наибольшему из полярных радиусов витка. К этому выводу пришел еще Архимед.

Длина дуги кривой в прямоугольных координатах

Пусть в прямоугольных координатах на плоскости дана кривая уравнением 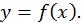Найдем длину дуги этой кривой. Возьмем на дуге точки с абсциссами

и проведем хорды

длины которых обозначим соответственно через Тогда получим ломаную вписанную в дугу Длина ломаной равна

Длино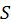й дуги называется тот предел, к которому стремится длина вписанной ломаной, когда длина ее наибольшего звена стемится к нулю:

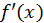Мы докажем сейчас, что если на отрезке функция и ее производная непрерывны, то этот предел существует. Вместе с тем будет дан и способ вычисления длины дуги.

Введем обозначения: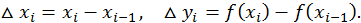

Тогда По теореме Лагранжа имеем:

где Следовательно,

Таким образом,

По условию 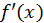непрерывна, следовательно, функция тоже непрерывна. Поэтому существует предел написанной интегральной суммы при условии, что 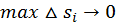(а значит и который равен определенному интегралу:

.

Итак, получили формулу для вычисления длины дуги:

Найдем теперь длину дуги кривой в том случае, когда уравнение кривой задано в параметрической форме:

где 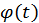и непрерывные функции с непрерывными производными, причем на

В этом случае эти уравнения определяют некоторую функцию непрерывную и имеющую непрерывную производную

Пусть Тогда, сделав в интеграле (7) подстановку получим:

Если задана пространственная кривая параметрическими уравнениями

то если непрерывны и имеют непрерывные производные на то

(без доказательства).

Поиск по сайту: