Первый способ

Задачи об отыскании условных экстремумов можно решать путем сведения их к задачам об отыскании абсолютных экстремумов функций, зависящих от меньшего числа переменных.

Суть этого метода на примере функции двух переменных, связанных одним условием, состоит в следующем.

Пусть требуется найти условные экстремумы функции

При условии, что и связаны уравнением

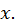При наличии условия из двух переменных и независимыми будет только одно, например так как определяется из равенства как функция от Разрешив уравнение относительно и вставив в равенство вместо найденное выражение, мы получим функцию одного переменного которую надо исследовать на абсолютный экстремум.

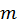Этот метод можно применять и при исследовании на условные экстремумы функции от большего числа переменных, например , связанных несколькими уравнениями, например Разрешая систему уравнений относительно каких-либо 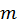переменных и подставляя эти выражения в функцию получим функцию от независимых переменных и придем к задаче отыскания абсолютных экстремумов функции, зависящей от переменных.

Но такое разрешение системы 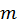уравнений часто бывает практически затруднительным и даже невыполнимым, поэтому был разработан другой метод решения этой задачи, который мы сейчас и рассмотрим

Поиск по сайту: