Второй способ.Метод множителей Лагранжа

Пусть требуется найти условные экстремумы функции

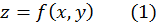
при условии, что и связаны уравнением

Будем решать теперь эту задачу, не разрешая уравнения относительно или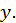

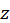При тех значениях при которых функция может иметь экстремум, производная от 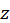по должна обращаться в нуль. Из находим помня, что есть функция от

Следовательно, в точках экстремума:

Из находим:

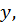Это равенство удовлетворяется для всех и удовлетворяющих уравнению

Умножив члены равенства 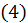на неопределенный пока коэффициент и сложив их с соответствующими членами равенства (3), получим:

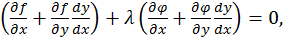
или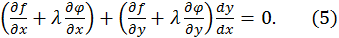

Последнее равенство выполняется во всех точках экстремума. Подберем так, чтобы для значений и 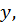соответствующих экстремуму функции 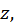вторая скобка в равенстве обращалась в нуль (для определенности будем предполагать, что в критических точках ):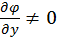

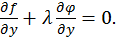
Но тогда при этих значениях и из равенства 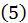следует равенство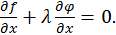

Таким образом, получается, что в точках экстремума удовлетворяются три уравнения:

с тремя неизвестными 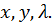Из этих уравнений определяем 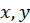и 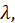которое играло только вспомогательную роль и нам в дальнейшем не требуется.

Из вывода следует, что уравнения 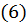являются необходимыми условиями условного экстремума, т.е. в точках экстремума удовлетворяются уравнения 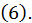Но не при всяких и (и ), удовлетворяющих уравнениям будет иметь место условный экстремум. Требуется дополнительное исследование характера критической точки. При решении конкретных задач иногда удается установить характер критической точки на основании существа задачи.

Заметим, что левые части уравнений 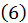есть частные производные функции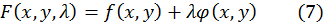

по переменным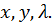

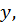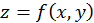Таким образом, для того чтобы найти значения и удовлетворяющие условию , при которых функция может иметь условный максимум или условный минимум, нужно составить вспомогательную функцию 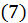, приравнять нулю ее производные по 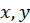и и из полученных трех уравнений 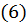определить искомые 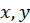и вспомогательный множитель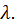

Рассмотренный метод распространяется на исследование условного экстремума функции переменных 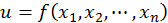при условии, что переменные 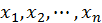связаны 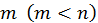уравнениями:

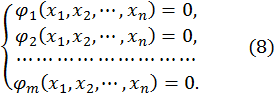
Составляем вспомогательную функцию:

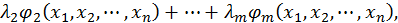
Приравниваем нулю ее частные производные по :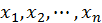

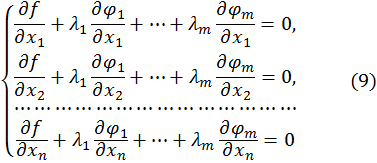
и из 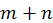уравнени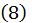й и 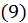определяем 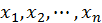и вспомогательные неизвестные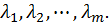

Так же как и для функции двух переменных, вопрос о том, будет ли при найденных значениях функция иметь условный экстремум или не будет иметь его, в общем случае остается открытым. Этот вопрос решается на основании вспомогательных соображений.

Пример. На плоскости найти точку, сумма квадратов расстояний которой от точек 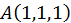и 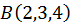была бы наименьшей.

Пусть искомая точка. Будем исследовать на экстремум функцию:

при условии:

Составляем вспомогательную функцию:

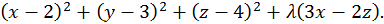
Приравнивая нулю частные производные, получаем систему четырех линейных уравнений с четырьмя неизвестными:

Решая эту систему, находим единственную критическую точку 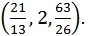Так как из геометрического смысла задачи следует, что наша функция должна иметь минимум, поэтому полученная критическая точка является точкой минимума.

Рекомендуемая литература

1. Пискунов Н.С. Дифференциальное и интегральное исчисления / Н.С. Пискунов. – М.: Наука, 1976. – Т.1.

2. Берман Г.Н. Сборник задач по курсу математического анализа / Г.Н. Берман. – М.: Наука, 2001.

3. Гусак А.А. Высшая математика / А.А. Гусак. – Минск: Изд-во БГУ, 1976. – Т.1.

4. Гусак А.А. Высшая математика / А.А. Гусак. – Минск: Изд-во БГУ, 1978. – Т.2.

Содержание

Приложения производной

Неопределенный интеграл 25

Определенный интеграл

Ряды

Функции нескольких переменных 83

Рекомендуемая литература

Поиск по сайту: