Необходимое условие интегрируемости функции

Теорема. Если функция интегрируема на отрезке то она и ограничена на этом отрезке.

Доказательство. Необходимость этого условия покажем, доказав утверждение: неограниченная на отрезке функция не интегрируема на этом отрезке.

В самом деле, если не ограничена на отрезке то она не ограничена на некотором элементарном отрезке За счет выбора точки интегральную сумму можно сделать сколь угодно большой, а такая интегральная сумма не имеет конечного предела.

Достаточно ли ограниченности функции для существования определенного интеграла? Оказывается, нет. Для того, чтобы доказать это, достаточно найти хотя бы один пример, показывающий, что интеграл для ограниченной функции не существует.

Вот такой пример. Функция Дирихле

На любом отрезке эта функция ограничена, но не является интегрируемой на нем. Действительно, если в каждом элементарном отрезке выбрать рациональную точку 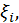то интегральная сумма Если выбрать иррациональную точку , то Предел интегральных сумм для функции Дирихле не существует, поэтому функция не является интегрируемой.

Отметим без доказательства, что справедливы следующие теоремы.

1. Если функция интегрируема на отрезке то она интегрируема на любом отрезке содержащемся в

2. Если функция непрерывна на отрезке то она и интегрируема на этом отрезке.

3. Если функция имеет на отрезке конечное число точек разрыва первого рода, то она интегрируема на

Поиск по сайту: