Теоремы о сравнении рядов с положительными членами

Пусть имеем два ряда с положительными членами:

Для них справедливы следующие теоремы.

Теорема 1. Если члены ряда не больше соответствующих членов ряда , т.е.

и ряд сходится, то сходится и ряд , причем его сумма не больше суммы ряда

Доказательство. Обозначим через и соответственно, е частичные суммы рядов и . Из 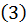следует, что

Так как ряд сходится, то существует Из того, что члены рядов и положительны, следует, что и тогда в силу неравенства 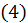Итак, последовательность частичных сумм возрастает (т.к. ее члены положительны) и ограничена сверху, следовательно, она имеет предел причем очевидно, что На основании этой теоремы можно судить о сходимости некоторых рядов.

Пример. Ряд

Сходится, т.к. его члены меньше соответствующих членов ряда

Но последний ряд сходится, т.к. его члены, начиная со второго, образуют геометрическую прогрессию со знаменателем . Сумма этого ряда равна . Следовательно, в силу теоремы 1, данный ряд тоже сходится, причем его сумма не превосходит .

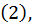Теорема 2. Если члены ряда не меньше соответствующих членов ряда т.е.

и ряд расходится, то и ряд расходится.

Доказательство. Из условия следует, что

Так как члены ряда положительны, то его частичная сумма 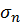возрастает при возрастании 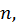а так как он расходится, то

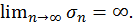Но тогда в силу неравенства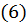 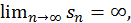т.е. ряд расходится.

Пример. Ряд

расходится, т.к. его члены (начиная со второго) больше соответствующих членов гармонического ряда который, как известно, расходится.

Замечание. Теоремы 1 и 2 справедливы и в случае, если неравенства или начинают выполняться лишь для а не для всех

Лекция 20.

Поиск по сайту: