Частные производные различных порядков

Пусть имеем функцию двух переменных: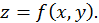

Частные производные и 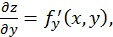вообще говоря, являются функциями переменных и 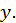Поэтому от них можно снова находить частные производные, которые называются производными второго порядка или вторыми производными. Их четыре:

Производные второго порядка можно снова дифференцировать как по так и по 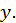Получим частные производные третьего порядка, которых будет уже восемь. Вообще, частная производная го порядка есть первая производная от производной го порядка.

Для функции любого числа переменных частные производные высших порядков определяются аналогично.

Естественно поставить вопрос, зависит ли результат дифференцирования функции нескольких переменных от порядка дифференцирования по разным переменным, т.е. будут ли, например, тождественно равны производные 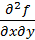и

Ответ дает следующая теорема.

Теорема. Если функция 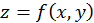и ее частные производные

и определены и непрерывны в точке и в некоторой ее окрестности, то в этой точке

Доказательство. Для доказательства рассмотрим выражение:

Если введем вспомогательную функцию определенную равенством: то можно записать в виде:

Так как, по предположению, определена в окрестности точки 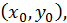то, следовательно, дифференцируема на отрезке но тогда, применяя теорему Лагранжа, получим:

где

Но

Так как определена в окрестности точки 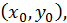применим к полученной разности вновь теорему Лагранжа (по переменному ):

где

Следовательно,

Переставив средние слагаемые в первоначальном выражении для получим:

Введем вспомогательную функцию: 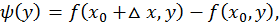тогда

Применяя снова теорему Лагранжа, получим:

где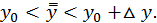

Но

Применив еще раз теорему Лагранжа, получим:

где

Таким образом,

Левые части равенств и равны, следовательно, равны и правые, т.е.

откуда

Переходя в этом равенстве к пределу при и получим:

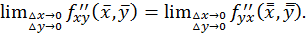
Так как производные и непрерывны в точке 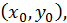то

и

Окончательно,

Что и требовалось доказать.

Из доказанной теоремы как следствие получается, что если частные производные и непрерывны, то они равны.

Аналогичная теорема имеет место и для функции любого числа переменных.

Лекция 26.

Поиск по сайту: