Экстремумы функции нескольких переменных

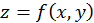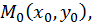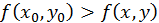Функция имеет максимум в точке если для всех точек достаточно близких к точке 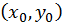и отличных от нее.

Функция 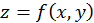имеет минимум в точке 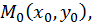если для всех точек достаточно близких к точке 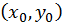и отличных от нее.

Из этих определений следует, что максимум и минимум функции нескольких переменных может достигаться лишь во внутренних точках области ее определения. Максимум и минимум функции называются экстремумами функции, т.е. говорят, что функция имеет экстремум в данной точке, если эта функция имеет максимум или минимум в данной точке.

Пример. Функция достигает минимума в точке Действительно, а так как при то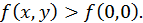

Теорема 1 (о необходимых условиях экстремума).

Если функция 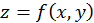достигает экстремума при то каждая частная производная первого порядка от 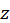или обращается в нуль при этих значениях аргументов, или не существует.

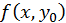Доказательство. Действительно, дадим переменному определенное значение, именно Тогда функция будет функцией одного переменного 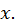Так как при она имеет экстремум, то, следовательно, или равно нулю, или не существует. Совершенно аналогично можно доказать, что или равно нулю, или не существует. Что и требовалось доказать.

Эта теорема не является достаточной для исследования вопроса об экстремальных значениях функции.

Точки, в которых (или не существует) и (или не существует), называются критическими точками функции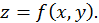

Если функция достигает экстремума в какой-либо точке, то (в силу теоремы 1) это может случиться только в критической точке.

Для исследования функции в критических точках существуют достаточные условия экстремума функции двух переменных.

Теорема 2 (о достаточных условиях экстремума).

Пусть в некоторой области, содержащей точку 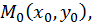функция 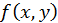имеет непрерывные частные производные до третьего порядка включительно; пусть, кроме того, точка является критической точкой функции т.е.

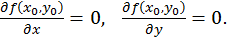
Тогда достаточные условия экстремума для функции 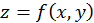выражаются с помощью определителя где

а именно:

1) если то точка экстремума:

при 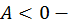точка максимума,

при точка минимума,

2) если то в точке нет экстремума,

3) если то экстремум может быть и может не быть (в этом случае требуется дальнейшее исследование функции, например, по знаку приращения функции вблизи этой точки).

Эту теорему примем без доказательства.

Поиск по сайту: