Метод подстановки

Пусть требуется найти интеграл причем непосредственно подобрать первообразную для мы не можем, но нам известно, что она существует. Сделаем замену переменной в подынтегральном выражении, положив

где 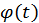– непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда докажем, что в этом случае имеет место следующее равенство:

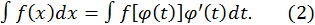
Здесь подразумевается, что после интегрирования в правой части равенства вместо будет подставлено его выражение через на основании равенства (1). Для того, чтобы установить, что выражения, стоящие в формуле (2) справа и слева, равны с точностью до произвольной постоянной, нужно доказать, что их производные по равны между собой.

Находим производную от левой части:

Правую часть равенства (2) будем дифференцировать по как сложную функцию, где - промежуточный аргумент. Зависимость от выражается равенством (1), при этом и по правилу дифференцирования обратной функции Таким образом имеем:

Что и требовалось доказать.

Функцию следует выбирать так, чтобы можно было вычислить неопределенный интеграл, стоящий в правой части равенства (2). Иногда целесообразнее подбирать замену переменного не в виде , а

Пример 1.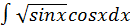

Сделаем подстановку тогда и, следовательно,

Пример 2.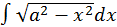

Сделаем подстановку тогда

Поиск по сайту: