 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Случай действительных корней знаменателя
Теорема 1. Пусть  есть действительный корень знаменателя кратности
есть действительный корень знаменателя кратности  т.е.
т.е.  где
где  тогда данную правильную дробь
тогда данную правильную дробь  можно представить в виде суммы двух других правильных дробей следующим образом:
можно представить в виде суммы двух других правильных дробей следующим образом:
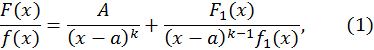
где  - постоянная, не равная нулю, а
- постоянная, не равная нулю, а  - многочлен, степень которого ниже степени знаменателя
- многочлен, степень которого ниже степени знаменателя 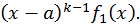
Доказательство. Напишем тождество:
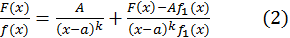
(справедливое при любом  ) и определим постоянную
) и определим постоянную  так, чтобы многочлен
так, чтобы многочлен  делился на
делился на  Для этого по теореме Безу необходимо и достаточно, чтобы выполнялось равенство:
Для этого по теореме Безу необходимо и достаточно, чтобы выполнялось равенство:
 Так как
Так как  то
то  однозначно определяется равенством:
однозначно определяется равенством:  При таком
При таком  будем иметь:
будем иметь:
 где
где  есть многочлен, степень которого ниже степени многочлена
есть многочлен, степень которого ниже степени многочлена 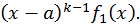 Сокращая последнюю дробь в формуле (2) на
Сокращая последнюю дробь в формуле (2) на  получаем равенство (1).
получаем равенство (1).
Следствие. К правильной рациональной дроби  входящей в (1), можно применить аналогичные рассуждения. Таким образом, если знаменатель имеет корень
входящей в (1), можно применить аналогичные рассуждения. Таким образом, если знаменатель имеет корень  кратности
кратности  то можно написать
то можно написать
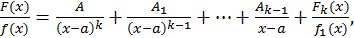
где  - правильная несократимая дробь. К ней также модно применить теорему 1, если
- правильная несократимая дробь. К ней также модно применить теорему 1, если 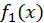 имеет другие действительные корни.
имеет другие действительные корни.
Поиск по сайту: