Необходимый признак сходимости ряда

Теорема. Если ряд сходится, то его й член стремится к нулю при неограниченном возрастании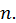

Доказательство. Пусть ряд

cходится, т.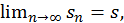е. где 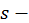сумма ряда (конечное фиксированное число); но тогда имеет место также равенство 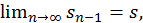т.к. при и

Вычитая почленно из первого равенства второе, получаем:

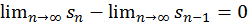или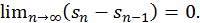

Но 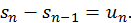Следовательно,

Что и требовалось доказать.

Следствие. Если й член ряда не стремится к нулю при то ряд расходится.

Пример. Ряд

расходится, т.к.

Рассмотренный признак является только необходимым, но не является достаточным, т.е. из того, что й член стремится к нулю, еще не следует, что ряд сходится, ряд может и расходиться.

Например, так называемый гармонический ряд

расходится, хотя

Расходимость гармонического ряда докажем позднее.

Поиск по сайту: