 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Дифференциал. Пусть функция дифференцируема на отрезке Производная этой функции в некоторой точке отрезка
Пусть функция  дифференцируема на отрезке
дифференцируема на отрезке  Производная этой функции в некоторой точке
Производная этой функции в некоторой точке  отрезка
отрезка  определяется равенством
определяется равенством 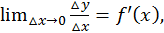 отсюда
отсюда 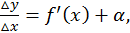 где
где 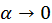 при
при  Умножая все члены последнего равенства на
Умножая все члены последнего равенства на 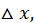 получим:
получим: 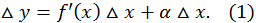
Так как в общем случае 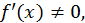 то при постоянном
то при постоянном  и переменном
и переменном  произведение
произведение  есть бесконечно малая величина первого порядка малости относительно
есть бесконечно малая величина первого порядка малости относительно 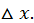 Произведение же
Произведение же 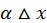 есть всегда величина бесконечно малая высшего порядка малости относительно
есть всегда величина бесконечно малая высшего порядка малости относительно 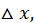 так как
так как 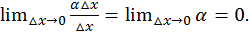
Таким образом, приращение 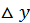 функции состоит из двух слагаемых, из которых первое слагаемое есть (при
функции состоит из двух слагаемых, из которых первое слагаемое есть (при  ) так называемая главная часть приращения, линейная относительно
) так называемая главная часть приращения, линейная относительно 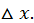 Эту главную часть приращения называют дифференциалом функции в точке
Эту главную часть приращения называют дифференциалом функции в точке  соответствующим приращению аргумента
соответствующим приращению аргумента 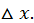 Принято обозначать дифференциал функции
Принято обозначать дифференциал функции  символом
символом  или
или 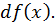
Итак, 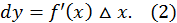
В случае  слагаемое
слагаемое  перестает быть главной частью приращения
перестает быть главной частью приращения 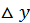 дифференцируемой функции (ибо это слагаемое равно нулю в то время, как слагаемое
дифференцируемой функции (ибо это слагаемое равно нулю в то время, как слагаемое  вообще говоря, отлично от нуля). Однако, договариваются и в случае
вообще говоря, отлично от нуля). Однако, договариваются и в случае  определять дифференциал функции формулой (2), т.е. считают, что он равен нулю в этом случае.
определять дифференциал функции формулой (2), т.е. считают, что он равен нулю в этом случае.
 Пример. Пусть функция
Пример. Пусть функция  есть площадь квадрата, сторона которого равна
есть площадь квадрата, сторона которого равна 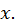 Если стороне
Если стороне  дать приращение
дать приращение 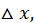 то новое ее значение станет
то новое ее значение станет  и, следовательно, площадь
и, следовательно, площадь  квадрата получит приращение
квадрата получит приращение  или
или  поэтому
поэтому  На рисунке приращение
На рисунке приращение 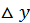 функции
функции  изображается площадью всей заштрихованной части, тогда как дифференциал
изображается площадью всей заштрихованной части, тогда как дифференциал  функции изображается площадью заштрихованной части без площади маленького квадрата, находящегося в правом верхнем углу большого квадрата.
функции изображается площадью заштрихованной части без площади маленького квадрата, находящегося в правом верхнем углу большого квадрата.
Введем понятие дифференциала независимой переменной. Под дифференциалом независимой переменной понимается дифференциал функции, тождественной с независимой переменной, т.е. функции  Поэтому
Поэтому  Тогда
Тогда 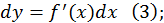
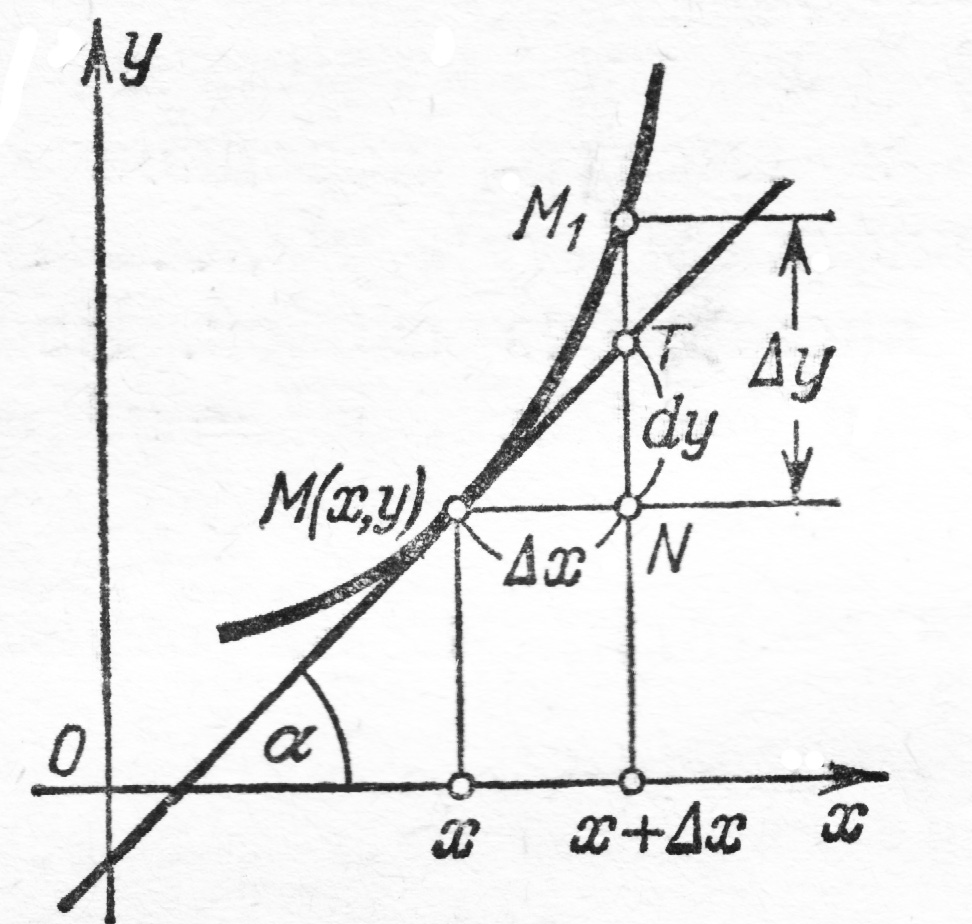
 откуда
откуда 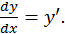
 Геометрический смысл дифференциала. Рассмотрим график функции
Геометрический смысл дифференциала. Рассмотрим график функции 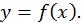 Пусть
Пусть  и
и  - две точки данной кривой. В точке
- две точки данной кривой. В точке  проведем касательную
проведем касательную  к графику функции и рассмотрим
к графику функции и рассмотрим  с катетами
с катетами  и
и  но из геометрического смысла производной следует
но из геометрического смысла производной следует  поэтому
поэтому  Т.о. дифференциал функции
Т.о. дифференциал функции  в данной точке
в данной точке  равен приращению ординаты касательной к графику функции в точке с абсциссой
равен приращению ординаты касательной к графику функции в точке с абсциссой  когда
когда  получает приращение
получает приращение 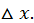
Если график функции вогнут, то  если же график функции выпукл, то
если же график функции выпукл, то 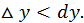
Физическое значение дифференциала. Пусть известен закон движения точки  по оси
по оси  где
где  - расстояние точки
- расстояние точки  от начала отсчета
от начала отсчета 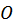 и
и  -время, причем будем предполагать, что точка
-время, причем будем предполагать, что точка  движется в одном и том же направлении. За бесконечно малый промежуток времени
движется в одном и том же направлении. За бесконечно малый промежуток времени  точка
точка  переместится в точку
переместится в точку  пройдя при этом путь
пройдя при этом путь  Это есть истинное приращение пути. Дифференциал пути
Это есть истинное приращение пути. Дифференциал пути 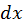 согласно формуле (3) равен
согласно формуле (3) равен  Но
Но  есть скорость движения
есть скорость движения  в момент времени
в момент времени  поэтому
поэтому  Таким образом, дифференциал пути равен тому фиктивному приращению пути, которое получится, если предположить, что начиная с данного момента времени, точка движется равномерно, сохраняя приобретенную скорость.
Таким образом, дифференциал пути равен тому фиктивному приращению пути, которое получится, если предположить, что начиная с данного момента времени, точка движется равномерно, сохраняя приобретенную скорость.
Например, если спидометр автомобиля показывает  то шофёр, рассчитывая, что за
то шофёр, рассчитывая, что за 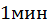 пробег машины составит
пробег машины составит  фактически вычисляет не приращение пути за
фактически вычисляет не приращение пути за  (которое вследствие неравномерности движения может быть не равно
(которое вследствие неравномерности движения может быть не равно  а дифференциал пути.
а дифференциал пути.
Поиск по сайту: