Признак Даламбера

Теорема. Если для ряда с положительными членами

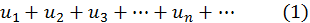
отношение - го члена к – му при имеет конечный предел т.е.

то: 1) ряд сходится в случае

2) ряд расходится в случае

(В случае ответа на вопрос о сходимости или расходимости ряда теорема не дает).

Доказательство. 1) Пусть Рассмотрим число Из определения предела и соотношения следует, что для всех значений 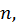начиная с некоторого номера т.е. для будет иметь место неравенство

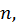Записывая для различных начиная с номера получим:

Рассмотрим теперь два ряда:

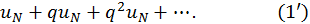
Ряд составлен из членов геометрической прогрессии с положительным знаменателем Следовательно, он сходится. Члены ряда начиная с меньше членов ряда На основании доказанного ранее следует, что ряд сходится.

2) Пусть Тогда из равенства (где ) следует, что начиная с некоторого номера т.е. для будет иметь место неравенство или для всех Но это означает, что члены ряда возрастают, начиная с номера 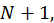и поэтому общий член ряда не стремится к нулю. Следовательно, ряд расходится.

Пример.

Следовательно, Ряд сходится.

Поиск по сайту: