Теоремы о сходимости рядов

Теорема 1. Если сходится ряд, получившийся из данного ряда отбрасыванием нескольких его членов, то сходится и сам данный ряд. Обратно, если сходится данный ряд, то сходится и ряд, получившийся из данного отбрасыванием нескольких членов.

Доказательство. Пусть сумма первых членов ряда сумма отброшенных членов при достаточно большом все отброшенные члены содержатся в сумме сумма членов ряда, входящих в сумму и не входящих в Тогда имеем: где постоянное число, не зависящее от 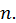Из последнего соотношения следует, что если существует то существует и если существует то существует и а это и доказывает справедливость теоремы.

Теорема 2. Если ряд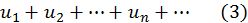

сходится и его сумма равна то ряд где 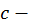какое-либо фиксированное число, также сходится и его сумма равна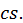

Доказательство. Обозначим ю частичную сумму ряда 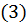через а ряда через Тогда

Отсюда ясно, что предел й частичной суммы ряда 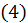существует, так как

Итак, ряд 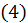сходится и его сумма равна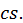

Теорема 3. Если ряды

и

сходятся и их суммы, соответственно, равны и 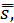то ряды

и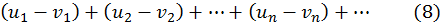

также сходятся и их суммы, соответственно, равны и

Доказательство. Докажем сходимость ряда Обозначая его ю частичную сумму через а е частичные суммы рядов и соответственно, через 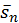и получим

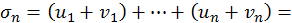
Переходя к пределу при получим:

Таким образом, ряд 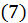сходится и его сумма равна

Аналогично доказывается, что ряд 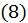также сходится и его сумма равна Про ряды 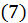и 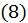говорят, что они получены в результате почленного сложения или, соответственно, почленного вычитания рядов и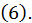

Поиск по сайту: