 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Дифференциал сложной функции нескольких переменных
Предположим, что в уравнении 
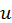 и
и  являются функциями независимых переменных
являются функциями независимых переменных  и
и 

В этом случае 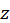 есть сложная функция от аргументов
есть сложная функция от аргументов  и
и 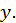
Конечно, 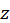 можно выразить и непосредственно через
можно выразить и непосредственно через  и
и 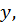 а именно:
а именно:

Предположим, что функции 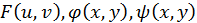 имеют непрерывные частные производные по всем своим аргументам и поставим задачу: вычислить
имеют непрерывные частные производные по всем своим аргументам и поставим задачу: вычислить 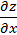 и
и 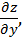 исходя из уравнений
исходя из уравнений  и
и  и не пользуясь уравнением
и не пользуясь уравнением 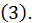
Дадим аргументу  приращение
приращение 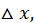 сохраняя значение
сохраняя значение  неизменным. Тогда, в силу уравнений
неизменным. Тогда, в силу уравнений 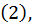
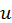 и
и  получат приращения
получат приращения  и
и  Но если
Но если 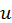 и
и  получают приращения
получают приращения  и
и 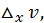 то и функция
то и функция  получит приращение
получит приращение  определяемое формулой:
определяемое формулой:
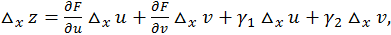
где  и
и 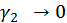 при
при  и
и 
Разделим все члены этого равенства на 

Если  то
то  и
и 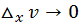 (в силу непрерывности функций
(в силу непрерывности функций 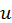 и
и 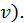 Но тогда
Но тогда  и
и  тоже стремятся к нулю. Переходя к пределу при
тоже стремятся к нулю. Переходя к пределу при  получим:
получим:

Если бы мы дали приращение 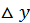 переменному
переменному 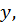 а
а  оставили неизменным, то с помощью аналогичных рассуждений нашли бы:
оставили неизменным, то с помощью аналогичных рассуждений нашли бы:
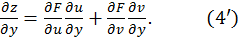
Для случая большего числа переменных формулы 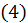 и
и  естественным образом обобщаются. Например, если
естественным образом обобщаются. Например, если  есть функция четырех аргументов
есть функция четырех аргументов 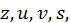 а каждый из них зависит от
а каждый из них зависит от  и
и 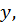 то формулы
то формулы 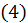 и
и  принимают вид:
принимают вид:
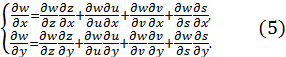
Если задана функция 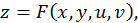 где
где 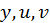 в свою очередь зависят от одного аргумента
в свою очередь зависят от одного аргумента 
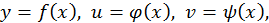 то, по сути дела,
то, по сути дела, 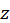 является функцией только одного переменного
является функцией только одного переменного  и можно ставить вопрос о нахождении производной
и можно ставить вопрос о нахождении производной  Эта производная вычисляется по первой из формул
Эта производная вычисляется по первой из формул 
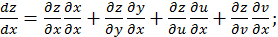
но так как  функции только одного аргумента
функции только одного аргумента  то частные производные обращабтся в обыкновенные, кроме того,
то частные производные обращабтся в обыкновенные, кроме того, 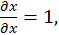 поэтому
поэтому
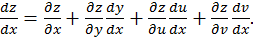
Эта формула носит название формулы для вычисления полной производной  (в отличие от частной производной
(в отличие от частной производной 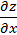 ).
).
Найдем далее полный дифференциал сложной функции, определенной равенствами  и
и  Подставим выражения
Подставим выражения 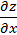 и
и 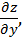 определенные равенствами
определенные равенствами 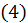 и
и 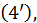 в формулу полного дифференциала:
в формулу полного дифференциала:

Получаем:

Произведем следующие преобразования в правой части:
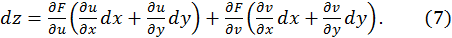
Но 
Равенство 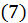 с учетом равенств
с учетом равенств 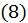 можно переписать так:
можно переписать так:

Сравнивая 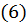 и
и 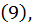 можем сказать, что выражение полного дифференциала функции нескольких переменных (дифференциала первого порядка) имеет тот же вид, т.е. форма дифференциала первого порядка инвариантна, являются ли
можем сказать, что выражение полного дифференциала функции нескольких переменных (дифференциала первого порядка) имеет тот же вид, т.е. форма дифференциала первого порядка инвариантна, являются ли 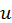 и
и  независимыми переменными или функциями независимых переменных.
независимыми переменными или функциями независимых переменных.
Поиск по сайту: