 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Свойства дифференциалов
Задача нахождения дифференциала функции равносильна нахождению производной, так как умножив последнюю на дифференциал аргумента, получим дифференциал функции. Следовательно, большинство теорем и формул, относящихся к производным, сохраняют силу и для дифференциалов.
1.Дифференциал постоянной равен нулю.
Полагая в формуле (3) 
и 
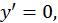получим 
2. Дифференциал алгебраической суммы нескольких дифференцируемых функций равен алгебраической сумме дифференциалов этих функций.
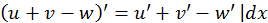
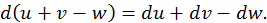
3. Если две дифференцируемые функции отличаются на постоянное слагаемое, то дифференциалы их равны между собой.
4. Постоянный множитель может быть вынесен за знак дифференциала.
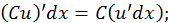
5. Дифференциал произведения.
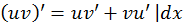
6. Дифференциал частного.
7. Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
Пусть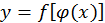 
. Положим 
и, следовательно, 
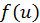Если 
и 
- дифференцируемые функции, то
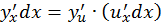или 
Из последней формулы следует такое свойство дифференциала.
8. Инвариантность формы первого дифференциала.
Дифференциал функции равен произведению производной этой функции на дифференциал аргумента, при этом безразлично, будет ли этот аргумент независимой переменной или дифференцируемой функцией от другой независимой переменной.
На основе формул для производных, можно получить соответствующие формулы для дифференциалов.
Например, 
и т.д.
Поиск по сайту: