Несобственные интегралы от разрывных функций

Пусть функция определена и непрерывна при а при терпит разрыв. Тогда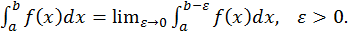

Если предел, стоящий справа существует, то несобственный интеграл называется сходящимся, а если не существует, то – расходящимся.

Аналогично, если определена и непрерывна при а при терпит разрыв, то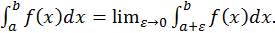

Если имеет разрыв в какой-нибудь промежуточной точке отрезка то по определению

Если оба интеграла в правой части сходятся, то сходится и интеграл этот интеграл расходится, если расходится хотя бы один из интегралов справа.

Пример 1. .

Пример 2. .

Вычислим каждый интеграл отдельно.

.

Следовательно, расходится.

Если бы мы стали вычислять данный интеграл, не обращая внимания на разрыв подынтегральной функции в точке то получили бы неверный результат: что невозможно.

Если 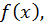определенная на имеет внутри этого отрезка конечное число точек разрыва то

если каждый из несобственных интегралов в правой части сходится. Если же хотя бы один из этих интегралов расходится, то и 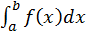тоже расходится.

Для определения сходимости несобственных интегралов от разрывных функций и оценки их значений часто могут быть применены теоремы, аналогичные тем, которые были для оценки интегралов с бесконечными пределами.

Теорема 1. Если на функции и разрывны только в точке причем во всех точках этого отрезка выполнены неравенства 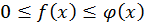и сходится, то 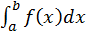также сходится, причем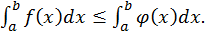

Теорема 2. Если на функции и разрывны только в точке причем во всех точках этого отрезка выполнены неравенства и расходится, то и 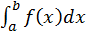расходится.

Теорема 3. Если знакопеременная функция на разрывная только в точке и сходится, то сходится и причем говорят, что он сходится абсолютно.

Пример. Сходится ли

сходится.

Следовательно, тоже сходится, причем он

Ряды