Свойства определенного интеграла

1. Эта формула рассматривается как соглашение. Она естественна с геометрической точки зрения. Так как основание криволинейной трапеции имеет длину, равную нулю, то и площадь этой криволинейной трапеции равна нулю.

2. Эта формула также рассматривается как соглашение. Она представляет собой естественное обобщение понятия интеграла на случай, когда отрезок при 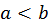пробегается в направлении от к (в этом случае в интегральной сумме все разности имеют отрицательный знак).

3. Постоянный множитель можно выносить за знак определенного интеграла: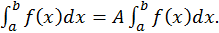

Доказательство.

4. Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов от слагаемых.

В случае двух слагаемых:

Доказательство аналогично предыдущему доказательству.

5. Если на отрезке где функции и удовлетворяют условию то

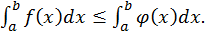
Доказательство. Рассмотрим разность:

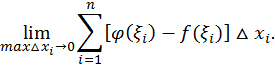
Здесь Следовательно, каждое слагаемое суммы неотрицательно, неотрицательна вся сумма и неотрицателен ее предел, т.е. откуда

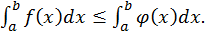Ч.т.д.

Если и то это свойство наглядно иллюстрируется геометрически. Так как то площадь криволинейной трапеции не больше площади криволинейной трапеции

6. Оценка определенного интеграла.

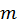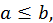Если и наименьшее и наибольшее значения функции на отрезке и то

Доказательство. По условию

На основании свойства 5 имеем:

Но

Подставляя, получим:

Если то это свойство легко иллюстрируется геометрически. Площадь криволинейной трапеции 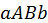содержится между площадями прямоугольников и

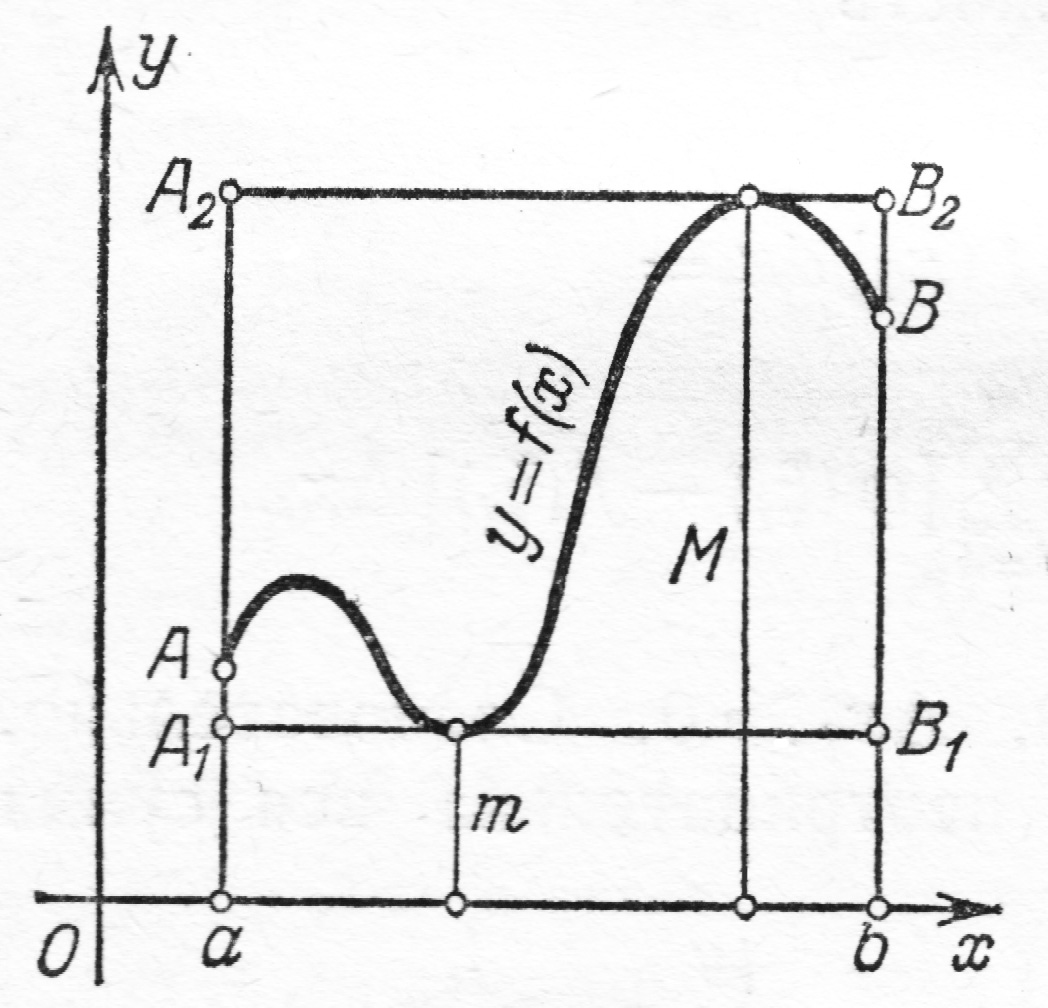7. Теорема о среднем.

Если функция непрерывна на отрезке то на этом отрезке найдется такая точка что справедливо следующее равенство:

Доказательство. Пусть для определенности В силу свойства 6:

Отсюда где

Так как непрарывна на то она принимает все промежуточные значения, заключенные между 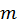и Следовательно, при некотором значении будет т.е.

8. Для любых трех чисел 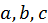справедливо равенство:

если только все эти три интеграла существуют.

Доказательство. Предположим сначала, что 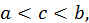и составим интегральную сумму для функции на отрезке Так как предел интегральной суммы не зависит от способа разбиения отрезка на части, то мы будем разбивать отрезок на малые отрезки так, чтобы точка была точкой деления. Разобьем далее интегральную сумму соответствующую отрезку на две суммы: сумму соответствующую отрезку и сумму соответствующую отрезку Тогда

Переходя к пределу при получим:

Если то на основании доказанного можем написать:

откуда с использованием свойства 2 получаем:

Аналогичным образом доказывается это свойство при любом другом расположении точек

На рисунке дана геометрическая иллюстрация свойства 8 для того случая, когда и площадь трапеции 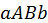равна сумме площадей трапеций и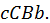

Лекция 16.

Поиск по сайту: