АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

По заданной скорости

Читайте также:
  1. IV. Современные методы синтеза неорганических материалов с заданной структурой
  2. Абсолютно неупругий удар. Абсолютно упругий удар. Скорости шаров после абсолютно упругого центрального удара.
  3. Влияние нагрева и скорости охлаждения углеродистой стали на ее структуру
  4. Влияние скорости охлаждения на формирование структуры
  5. Влияние скорости процессов на надежность технических систем
  6. Волновой пакет. Возможные скорости(4 штуки). Скорость переноса энергии. Связь групповой скорости с фазовой. Дисперсия упругих волн.
  7. Вопрос 40. Расчет пройденного расстояния, времени полета и путевой скорости по маршруту АП-1 – АП-2.
  8. Вопрос№5 Движение по окружности. Связь угловой и линейной скорости
  9. Выбор и обоснование маневра для расхождения в заданной дистанции.
  10. Выбор шага интегрирования по заданной точности.
  11. Задача синтеза информационной системы заданной стоимости
  12. Задача стабилизации скорости вращения электродвигателя

Пусть точка движется прямолинейно с переменной скоростью Вычислим длину пути, пройденного точкой за промежуток времени от до

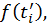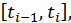Промежуток разобьем произвольным образом на элементарных промежутков длины В течение малого промежутка времени скорость движения можно приближенно считать постоянной и равной где некоторое произвольное значение из перомежутка поэтому длина пути, пройденного за этот промежуток приближенно равна Складывая все частные длины получаем приближенное значене длины пути, пройденного точкой за промежуток от до

Переходя к пределу при находим точное значение длины пути и в то же время получаем определенный интеграл от функции на отрезке :

Таким образом, физический смысл определенного интеграла состоит в том, что если скорость прямолинейного движения, то определенный интеграл (4) дает длину пути, пройденного за промежуток времени от до


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)