Теорема о необходимом признаке точки перегиба

Если 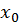- абсцисса точки перегиба графика дифференцируемой функции то либо либо не существует.

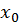
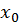Доказательство. Мы определили точку перегиба, как такую точку графика, которая отделяет выпуклую часть непрерывной кривой от вогнутой. Из доказанной выше теоремы о необходимом условии вогнутости (выпуклости) графика функции следует, что с одной стороны от точки а с другой таким образом, точка разделяет два интервала монотонности функции 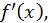следовательно, она является точкой экстремума для функции Применяя теорему о необходимом условии экстремума функции, получаем, что если 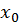– абсцисса точки перегиба, то либо равняется нулю, либо не существует.

Те точки в которых или не существует, называются критическими точками второго рода для функции 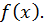Критическая точка второго рода не обязательно должна быть абсциссой точки перегиба, но только среди критических точек второго рода надо искать абсциссы точек перегиба.

Поиск по сайту: