 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
От выбора аргумента. Непосредственное интегрирование
В таблице неопределенных интегралов предполагалось, что 
есть независимая переменная. Однако, эта таблица полностью сохраняет свое значение, если под понимать любую дифференцируемую функцию от независимой переменной.
В самом деле, пусть есть независимая переменная, 
- некоторая непрерывная функция на данном промежутке и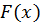 
– ее первообразная, т.е. 
Имеем
Пусть 
- дифференцируемая функция . В силу инвариантности формы первого дифференциала
откуда
.
Итак, из справедливости формулы (1) следует справедливость формулы (2), которая получается из первой формулы формальной заменой на 
На основании этого свойства получаем обобщенную таблицу простейших интегралов:
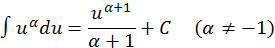
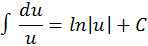
и т.д.,
где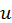 
-любая дифференцируемая функция .
Пример. 
.
Заменяя на 
получим:
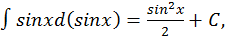
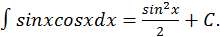
Отсюда становится понятной важность умения приводить данное дифференциальное выражение 
к виду: 
где 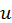есть некоторая функция от и 
- функция более простая для интегрирования, чем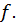 
Отметим ряд преобразований дифференциала, полезных для дальнейшего:
1) 
где 
- постоянная величина
2) 
где постоянная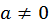 
3) 
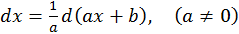
4) 
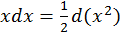
5) 
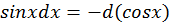
Вообще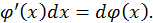 
Пользуясь этими преобразованиями дифференциалов, найдем некоторые неопределенные интегралы. Такой способ интегрирования называется непосредственным интегрированием.
Пример 1.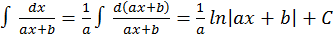 
Пример 2.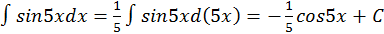 
Пример 3.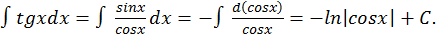 
Лекция 8.
Поиск по сайту: