Интегралы от иррациональных функций

Не от всякой иррациональной функции интеграл выражается через элементарные функции. Рассмотрим некоторые иррациональные функции, интегралы от которых с помощью подстановок приводятся к интегралам от рациональных функций и, следовательно, до конца интегрируются.

1. Рассмотрим интеграл

где 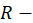рациональная функция своих аргументов, т.е. над величинами производятся только рациональные операции.

Пусть общий знаменатель дробей Сделаем подстановку:

Тогда каждая дробная степень выразится через целую степень и, следовательно, подынтегральная функция преобразуется в рациональную функцию от

Пример. Общий знаменатель дробей есть , поэтому

2. Рассмотрим интеграл

Этот интеграл преобразуется в интеграл от рациональной функции с помощью подстановки где общий знаменатель дробей .

Поиск по сайту: