 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теорема о достаточном признаке возрастания (убывания) функции
1) Если производная дифференцируемой функции положительна внутри некоторого промежутка, то функция возрастает на этом промежутке.
2) Если производная дифференцируемой функции отрицательна внутри некоторого промежутка, то функция убывает на этом промежутке.
 Доказательство. 1) Пусть дифференцируемая функция
Доказательство. 1) Пусть дифференцируемая функция  такова, что
такова, что  при
при 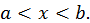 Для любых двух значений
Для любых двух значений 
 в силу теоремы Лагранжа о конечных приращениях имеем
в силу теоремы Лагранжа о конечных приращениях имеем  где ξ – промежуточное значение между
где ξ – промежуточное значение между 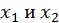 и, следовательно, лежащее в
и, следовательно, лежащее в 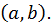 так как
так как  и
и  то отсюда получим
то отсюда получим  или
или  Следовательно, функция
Следовательно, функция  возрастает на отрезке
возрастает на отрезке 
2) Доказательство второй части этой теоремы совершенно аналогично доказательству первой ее части (провести самим!).
Функция возрастающая или убывающая называется монотонной. Промежутки, в которых данная функция возрастает или убывает, называются промежутками монотонности этой функции.
Пример. Определить промежутки монотонности функции 
Производная равна  при
при 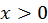 имеем
имеем  - функция возрастает; при
- функция возрастает; при 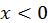 имеем
имеем  - функция убывает.
- функция убывает.
Поиск по сайту: