АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Основные методы интегрирования

Читайте также:
  1. B. Основные принципы исследования истории этических учений
  2. I. ОСНОВНЫЕ ПОНЯТИЯ (ТЕРМИНЫ) ЭКОЛОГИИ. ЕЕ СИСТЕМНОСТЬ
  3. I.3. Основные этапы исторического развития римского права
  4. II Съезд Советов, его основные решения. Первые шаги новой государственной власти в России (октябрь 1917 - первая половина 1918 гг.)
  5. II. Методы непрямого остеосинтеза.
  6. II. Основные задачи и функции
  7. II. Основные показатели деятельности лечебно-профилактических учреждений
  8. II. Основные проблемы, вызовы и риски. SWOT-анализ Республики Карелия
  9. II. Рыночные методы.
  10. III. Параметрические методы.
  11. IV. Механизмы и основные меры реализации государственной политики в области развития инновационной системы
  12. IV. Современные методы синтеза неорганических материалов с заданной структурой

Для вычисления данного интеграла мы должны, если это возможно, пользуясь теми или иными способами, привести его к табличным интегралам и таким образом найти искомый результат. Рассмотрим основные методы интегрирования.

1. Метод разложения.

Пусть

Тогда на основании четвертого свойства неопределенного интеграла имеем

По возможности слагаемые 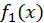и стараются подобрать так, чтобы интегралы от них находились непосредственно.

Пример 1.

Нет надобности после каждого слагаемого ставить произвольную постоянную, потому что сумма произвольных постоянных есть также произвольная постоянная, которую мы пишем в конце.

Пример 2.

Пример 3.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)