Теорема 2 о достаточных условиях существования экстремума

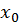Если для дифференцируемой функции в некоторой точке ее первая производная 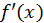равна нулю, а вторая производная существует и отлична от нуля, т.е. то в этой точке функция имеет экстремум, а именно:

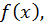1) если то - минимум функции и

2) если 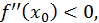то - максимум функции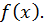

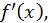Доказательство. 1) Пусть Пусть - точка, близкая к Так как есть производная от то (здесь мы воспользовались тем, что 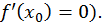Таким образом, переменная величина стремится к пределу а значит в некоторой окрестности точки 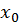эта величина имеет знак своего предела (на основании теоремы о сохранении знака функции), т.е. в нашем случае знак плюс. Поэтому при Отсюда получаем, что числитель и знаменатель дроби имеют одинаковые знаки и, следовательно, и

Мы видим, что производная 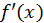при переходе через точку 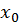меняет свой знак с минуса на плюс. На основании теоремы 1 число есть минимум функции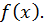

2) Аналогично доказывается, что если то - максимум функции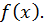

Для запоминания связи между знаком второй производной и максимумом и минимумом функции можно использовать так называемое правило дождя .

Лекция 3

Поиск по сайту: