Геометрическая интерпретация

Комплексное число будем изображать точкой с прямоугольными координатами и 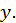Ось абсцисс называется действительной осью, ось ординат - мнимой осью. Очевидно, что нами установлено взаимно-однозначное соответствие между множеством всех комплексных чисел и множеством всех точек плоскости, которая называется комплексной плоскостью. Вследствие этого в дальнейшем мы не будем делать различия в терминах 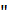комплексное число , 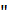точка .

Введем на нашей плоскости полярную систему координат

Так что Получили тригонометрическую форму комплексного числа Положительное число называется модулем комплексного числа 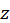и обозначается Угол 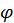называется аргументом комплексного числа и обозначается Очевидно, если комплексное число задано (в алгебраической форме), то его аргумент однозначно не определен, а лишь с точностью до слагаемого 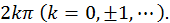Поэтому вводят в рассмотрение главное значение аргумента: - это то значение угла которое заключено в пределах одного оборота: Тогда

Равенство комплексных чисел и в тригонометрической форме выглядит так (точки на плоскости совпадают!): и (или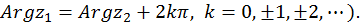

Условие сопряженности комплексных чисел (которые изображаются симметричными относительно действительной оси точками) такое:

Умножение комплексных чисел в тригонометрической форме:

Деление комплексных чисел в тригонометрической форме:

Возвышение в n-ю степень (n – целое положительное число):

Извлечение корня n-ой степени.

Число называется корнем n-ой степени из комплексного числа 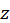, если Пишем так:

Если (𝜌 и ψ нам пока неизвестны), то или (*)

Полагая получим Если далее положить то получим Видно, что все остальные получаются из написанных путем прибавления слагаемых, кратных 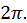Так что (*) определяет различных значений

Эти точки делят окружность радиуса на равных частей.

Пример. Найти все значения

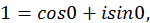
Полагая 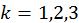, находим три значения корня:

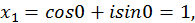
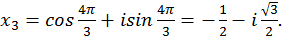
Лекция 10.

Поиск по сайту: