АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Наибольшее и наименьшее значения функции на отрезке

Читайте также:
  1. II. Основные задачи и функции
  2. III. Используемые определения и обозначения
  3. III. Предмет, метод и функции философии.
  4. IV. Конструкция бент-функции
  5. Ms Excel: мастер функций. Логические функции.
  6. S: Определить длину отрезка, на котором укладывается столько же длин волн в вакууме, сколько их укладывается на отрезке 3 мм в воде.
  7. V2: ДЕ 29 - Введение в анализ. Предел функции на бесконечности
  8. V2: ДЕ 32 - Дифференциальное исчисление функции одной переменной. Производная
  9. V2: ДЕ 35 - Дифференциальное исчисление функции одной переменной. Производные высший порядков
  10. V2: ДЕ 39 - Интегральное исчисление функции одной переменной. Приложения определенного интеграла
  11. V2: Функции исторической науки
  12. VIII. ФУНКЦИИ НАУЧНОГО ИССЛЕДОВАНИЯ

Пусть функция непрерывна на отрезке Тогда на этом отрезке функция достигает наибольшего значения. Будем предполагать, что на данном отрезке функция имеет конечное число критических точек первого рода. Если наибольшее значение достигается внутри отрезка то, очевидно, что это значение будет одним из максимумов функции (если имеется несколько максимумов), а именно, наибольшим максимумом. Но может случиться, что наибольшее значение будет достигаться на одном из концов отрезка. То же самое можно сказать и о наименьшем значении функции: оно достигается либо на одном из концов данного отрезка, либо в такой внутренней точке, которая является точкой наименьшего минимума.

Таким образом, если требуется найти наибольшее значение непрерывной функции на отрезке то надо: найти все максимумы функции на отрезке, определить значения функции на концах отрезка и из всех полученных выше значений функции выбрать наибольшее. Аналогичным образом следует поступать и при определении наименьшего значения функции на отрезке.

Пример. Определить на отрезке 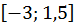наибольшее и наименьшее значения функции

следовательно, в точке минимум следовательно, в точке максимум Определяем значения функции на концах отрезка:

Таким образом, наибольшее значение рассматриваемой функции на 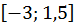наименьшее значение

 

Лекция 5.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)