 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тригонометрических функций
Интеграл вида 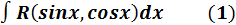
Этот интеграл с помощью подстановки 
всегда сводится к интегралу от рациональной функции.
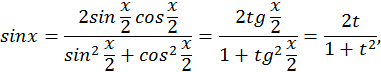

Далее, 
Таким образом,  и
и  выразились рационально через
выразились рационально через  Подставляя полученные выражения в
Подставляя полученные выражения в  получим интеграл от рациональной функции.
получим интеграл от рациональной функции.
Пример. 
Рассмотренная подстановка дает возможность проинтегрировать всякую функцию вида 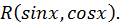 Поэтому ее называют
Поэтому ее называют 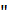 универсальной тригономнтрической подстановкой
универсальной тригономнтрической подстановкой  Однако, на практике она часто приводит к слишком сложным рациональным функциям. Поэтому наряду с
Однако, на практике она часто приводит к слишком сложным рациональным функциям. Поэтому наряду с  универсальной
универсальной  подстановкой бывает полезно знать также другие подстановки, которые в некоторых случаях быстрее приводят к цели.
подстановкой бывает полезно знать также другие подстановки, которые в некоторых случаях быстрее приводят к цели.
1) Если интеграл имеет вид  то подстановка
то подстановка 
 приводит этот интеграл к виду
приводит этот интеграл к виду 
2) Если интеграл имеет вид 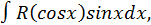 то подстановка
то подстановка 
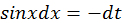 приводит его к виду
приводит его к виду 
3) Если интеграл имеет вид  то подстановка
то подстановка 

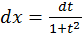 приводит его к виду
приводит его к виду 
4) Если интеграл имеет вид  но
но  и
и  входят только в четных степенях, то применяется подстановка
входят только в четных степенях, то применяется подстановка  т.к.
т.к.  и
и  выражаются рационально через
выражаются рационально через 


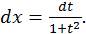 После подстановки получим интеграл от рациональной функции.
После подстановки получим интеграл от рациональной функции.
5) Пусть интеграл имеет вид  где
где 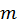 и
и  целые числа. Рассмотрим три случая.
целые числа. Рассмотрим три случая.
 и
и  таковы, что по крайней мере одно из них нечетное число. Допустим для определенности, что
таковы, что по крайней мере одно из них нечетное число. Допустим для определенности, что  нечетное. Положим
нечетное. Положим 
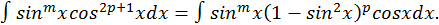
Сделаем замену 

 и
и  числа неотрицательные и четные.
числа неотрицательные и четные.
Положим 
 ,
, 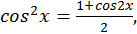
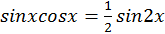
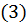

Возводя в степень и раскрывая скобки, получим члены, содержащие  в нечетных и четных степенях. Члены с нечетными степенями интегрируются, как указано в случае
в нечетных и четных степенях. Члены с нечетными степенями интегрируются, как указано в случае  Четные показатели степеней снова понижаем по формулам
Четные показатели степеней снова понижаем по формулам 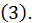 Продолжая так, дойдем до членов вида
Продолжая так, дойдем до членов вида  которые легко интегрируются.
которые легко интегрируются.
 и
и  числа четные, причем хотя бы одно из них отрицательно.
числа четные, причем хотя бы одно из них отрицательно.
В этом случае предыдущий прием не проходит и приходится поступать как в пункте 4), т.е. делать подстановку  или
или 
6) Рассмотрим интегралы вида: 


Они берутся при помощи следующих формул 



Подставляя и интегрируя, получим


Аналогично вычисляются и два других интеграла.
Интеграл вида 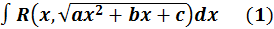
(тригонометрические подстановки)
Предполагается, что 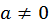 и
и 
Покажем метод преобразования этого интеграла к интегралу вида

который был рассмотрен нами.

Сделаем замену: 
Тогда 
Рассмотрим все возможные случаи.
1. Пусть  Введем обозначения
Введем обозначения 

2. Пусть  Тогда
Тогда 

3. Пусть  Тогда
Тогда 

4. Пусть  В этом случае
В этом случае 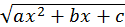 есть комплексное число при любом значении
есть комплексное число при любом значении 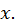
Таким образом, интеграл (1) преобразуется к одному из следующих типов.
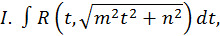


Интеграл I типа приводится к интегралу вида (2) с помощью подстановки 
Для интеграла II типа нужно применить подстановку 
А в интеграле III типа следует сделать подстановку 
Пример.  Это интеграл III типа. Делаем подстановку
Это интеграл III типа. Делаем подстановку 


Поиск по сайту: