Несобственные интегралы с бесконечными пределами

Пусть функция определена и непрерывна при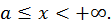

Несобственным интегралом от функции с бесконечным верхним пределом называется интеграл

если предел, стоящий справа, существует. Говорят, что в этом случае несобственный интеграл существует или сходится. Если же этот предел не существует, то говорят, что несобственный интеграл не существует или расходится.

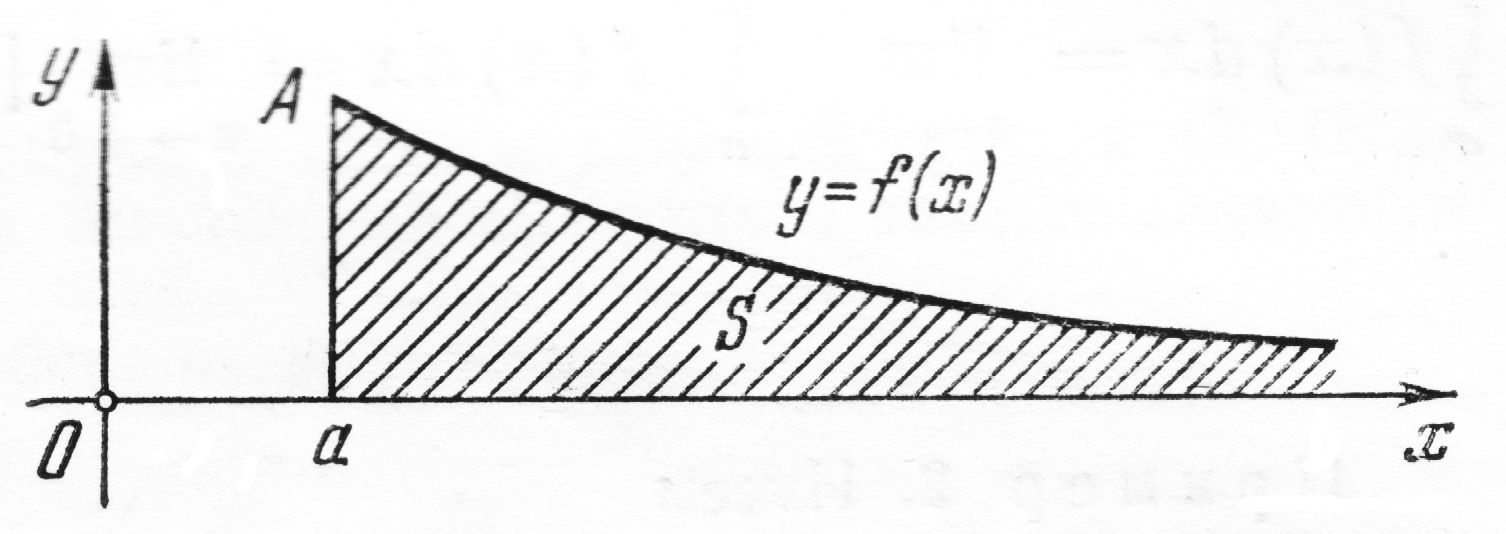Легко выяснить геометрический смысл несобственного интеграла в случае, когда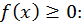 выражает площадь неограниченной (бесконечной) области, заключенной между линиями 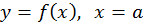и осью абсцисс.

Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:

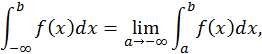
где 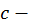любое конечное число.

Последнее равенство следует понимать так: если каждый из несобственных интегралов, стоящих справа, существует, то существует и интеграл, стоящий слева.

Пример. Вычислить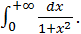

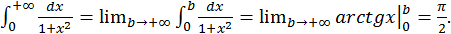
Во многих случаях бывает достаточно установить, сходится данный интеграл или расходится, и оценить его значение. Для этого могут быть полезными следующие теоремы, которые мы примем без доказательства, а применение их рассмотрим на примерах.

Теорема 1. Если для всех 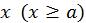выполняются неравенства и если сходится, то также сходится, при этом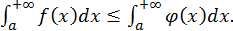

Пример. Исследовать, сходится ли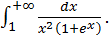

Заметим, что при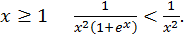

Далее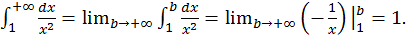

Следовательно, сходится и его значение

Теорема 2. Если для всех 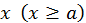выполняются неравенства причем расходится, то расходится и интеграл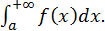

Пример. Исследовать, сходится ли

Замечаем, что

Но

Следовательно, расходится и данный интеграл.

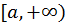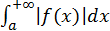Теорема 3. Если знакопеременная функция на и сходится, то сходится и причем говорят, что он сходится абсолютно.

Пример. Исследовать сходимость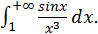

Здесь подынтегральная функция – знакопеременная. Замечаем, что 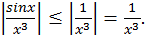Но

Следовательно, сходится. Отсюда следует, что сходится и данный интеграл, причем абсолютно.

Поиск по сайту: