Первообразная и неопределенный интеграл. До сих пор мы рассматривали такую задачу: дана функция требуется найти ее производную, т.е

До сих пор мы рассматривали такую задачу: дана функция требуется найти ее производную, т.е. функцию

Теперь мы будем рассматривать обратную задачу: дана функция требуется найти такую функцию 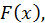производная которой равна 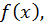т.е.

Определение 1. Функция 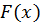называется первообразной от функции на отрезке если во всех точках этого отрезка выполняется равенство

Пример. Найти первообразную от функции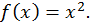

Из определения первообразной следует, что функция является первообразной,т.к. Легко видеть, что если для данной функции существует первообразная, то эта первообразная не является единственной. Так в рассматриваемом примере можно было взять в качестве первообразных следующие функции:

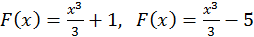или вообще (где - произвольная постоянная), т.к.

С другой стороны, можно доказать, что функциями вида исчерпываются все первообразные от функции 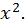Это вытекает из следующей теоремы.

Теорема. Если и - две первообразные от функции на отрезке то разность между ними равна постоянному числу.

Доказательство. Имеем: (1)

при любом значении на отрезке

Обозначим:

Тогда на основании (1) будет:

или при любом значении на отрезке Но из равенства следует, что есть постоянная. Обозначая эту постоянную через 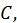из (2) получаем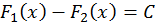

Из доказанной теоремы следует, что если для данной функции найдена какая-нибудь одна первообразная 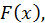то любая другая первообразная для имеет вид где

Определение 2. Если функция 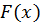является первообразной для 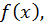то выражение называется неопределенным интегралом от функции и обозначается символом 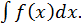Иначе, неопределенным интегралом от функции называется множество всех ее первообразных.

Таким образом, по определению

если

При этом функцию называют подынтегральной функцией, - подынтегральным выражением, знак ∫ - знаком интеграла.

Таким образом, неопределенный интеграл представляет собой семейство функций С геометрической точки зрения неопределенный интеграл представляет семейство кривых, каждая из которых получается путем сдвига одной из кривых параллельно самой себе вверх или вниз, т.е. вдоль оси

Первообразные (а значит и неопределенный интеграл) существуют не для всякой функции 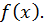Заметим, однако, без доказательства, что если функция непрерывна на отрезке то для этой функции существует первообразная (а значит и неопределенный интеграл).

Нахождение первообразной для данной функции называется интегрированием функции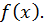

Поиск по сайту: